Оптическая длина пути. Оптическая разность хода.

Пусть в некоторой точке пространства О волна делится на две когерентные. Одна из них проходит путь S₁ в среде с показателем преломления n₁, а вторая – путь S₂ в среде с показателем n₂, после чего волны накладываются в точке Р. Если в данный момент времени t фазы волны в точке О одинаковы и равны j₁=j₂=wt, то в точке Р фазы волн будут равны соответственно

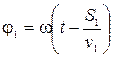и ,

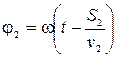где v₁ и v₂- фазовые скорости в средах. Разность фаз δ в точке Р будет равна

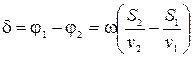(2)

При этом v₁=c/n₁, v₂=c/n₂. Подставляя эти величины в (2), получим

.

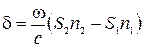Поскольку , где l₀– длина волны света в вакууме, то

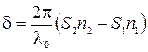(3)

Оптической длиной пути L в данной среде называется произведение расстояния S, пройденного светом в среде, на абсолютный показатель преломления среды n:

L = S n.

Таким образом, из (3) следует, что изменение фазы определяется не просто расстоянием S, а оптической длиной пути L в данной среде. Если волна проходит несколько сред, то L=Σn_iS_i. Если среда является оптически неоднородной (n≠const), то .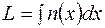

Величину δ можно представить в виде:

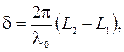
где L₁ и L₂ – оптические длины пути в соответствующих средах.

Величину, равную разности оптических длин путей двух волн Δ_опт = L₂ - L₁

называют оптической разностью хода. Тогда для δ имеем:

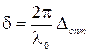
Сопоставление оптических длин пути двух интерферирующих волн позволяет предсказать результат их интерференции. В точках, для которых

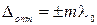
будут наблюдаться максимумы (оптическая разность хода равна целому числу длин волн в вакууме). Порядок максимума m показывает, сколько длин волн в вакууме составляет оптическая разность хода интерферирующих волн. Если же для точек выполняется условие

,

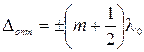то в них будут наблюдаться минимумы (оптическая разность хода равна нечетному числу половин длин волн).