Кольца Ньютона.

Частный случай полос равной толщины - кольца Ньютона - наблюдаются, если плосковыпуклую линзу поместить на плоскопараллельную стеклянную пластинку (рис 3).

Если на линзу падает пучок монохроматического света, то световые волны, отражённые от воздуха в точке А и от стекла в точке В(т.е. от верхней и нижней границ воздушной прослойки), оказываются когерентными и интерферируют. Волна, отраженная от плоской поверхности линзы, не когерентна с ними и дает лишь равномерную засветку. Точки, для которых толщина воздушного зазора одинакова, располагаются на окружностях, поэтому интерференционная картина имеет вид чередующихся концентрических темных и светлых колец.

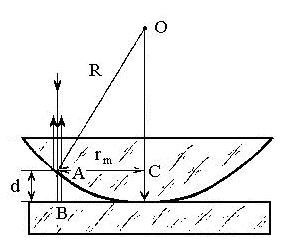
Рис.3. Схема возникновения колец Ньютона

Так как отражение световой волны в точке В происходит от стекла (оптически более плотной среды), то оптическая длина пути второго луча в точке А составит АВ + ВА + λ/2. Оптическая длина пути первого луча в точке А равна нулю. Поэтому

Δ_опт = L₂- L₁ = АВ + ВА + λ/2 = 2d + λ / 2

Тёмные кольца образуются там, где оптическая разность хода равна нечётному числу полуволн:

Δ_опт = 2d + λ /2 = (2m + 1) λ /2,

т.е. при толщине зазора

d = m λ /2 , (8)

где m = 0,1,2,3... - номер кольца.

В центре интерференционной картины находится темный круг, соответствующий минимуму нулевого порядка. Если r_m - радиус темного кольца под номером m, то из треугольника AОС (см. рис.3) имеем:

r_m^{2 =} R² - (R - d,)² = 2Rd – d ², (9)

где R - радиус кривизны линзы. Полагая величину воздушного зазора в месте возникновения колец малой, (т.е. пренебрегая d ² по сравнению с 2Rd), получим:

r_m ² = 2Rd. .

Подставляя сюда (8), получим

r_m² = Rmλ (10)

Из этой формулы видно, что зная длину волны используемого света радиус кривизны линзы можно найти путем измерения радиуса кольца Ньютона и определения его порядкового номера.

Использование формулы (10) для определения радиуса кривизны может привести к ошибке, т.к. в точке соприкосновения линзы и стеклянной пластинки возможна деформация, как линзы, так и пластинки, сравнимая по величине с длиной волны света. Поэтому результаты, полученные без учета этого факта, являются неточными.

Величина воздушного зазора оказывается меньше теоретической величины, полученной из рис.3, на величину суммарной деформации стеклянной пластинки и линзы δ (рис.4). Учитывая это, в формулу (9) вместо толщины воздушного зазора d необходимо подставить сумму толщины воздушного зазора и величины суммарной деформации линзы и стеклянной пластинки (d + δ):

r_m^{2 =} R² – [R –(d+ δ)]².

Пренебрегая малой величиной (d+ δ)², получаем:

r_m² = 2R(d + δ )

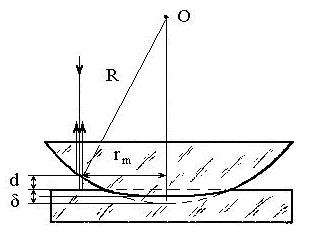
Рис.4. Учет деформации линзы и стеклянной пластинки

Учитывая (13), получим следующую формулу, для радиусов темных колец Ньютона с учетом суммарной деформации:

r_m² = Rmλ + 2Rδ (11)

Экспериментально удобнее вместо радиуса кольца Ньютона измерять его диаметр (D_m ). В этом случае формула (11) будет иметь вид:

D_m² = 4Rmλ + 8Rδ, (12)

Из (12) видно, что квадрат диаметра кольца Ньютона D_m² пропорционален порядковому номеру кольца m. Если построить график зависимости D_m² от m, то экспериментальные точки должны лежать на одной прямой, и тангенс угла наклона этой прямой tgα будет равен 4Rλ. Таким образом, для нахождения радиуса кривизны линзы необходимо, используя график зависимости D_m² = f(m), найти

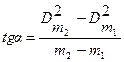, (13)

где m₁, m₂ номера колец,

D²_m1 и D²_m2 – их диаметры,

Радиус кривизны линзы затем можно рассчитать по формуле

R=tgα/4λ. (14)

В центре линзы наблюдается круглое темное пятно, соответствующее нулевой толщине воздушного зазора в области деформации. Измерив диаметр центрального темного пятна (т.е. темного кольца, номер которого m=0), из (12) можно найти величину суммарной деформации линзы и стеклянной пластинки по формуле:

δ = D₀²/ ( 8R ) (15)