Временная и пространственная когерентность.

Под когерентностью понимают согласованное протекание волновых или колебательных процессов. Различают временную и пространственную когерентность. Под временной когерентностью понимают степень согласованности колебаний в некоторой точке пространства с течением времени. Эта согласованность нарушается с течением времени для излучения обычных источников из-за того, что, как отмечалось выше, световая волна представляет собой суперпозицию огромного числа цугов. Пока излучают одни и те же атомы, фаза суммарной волны остается постоянной. Однако с течением времени одни атомы прекращают излучение и соответствующие им цуги исчезают. Другие атомы, наоборот, начинают излучать, и возникают новые цуги, фазы которых никак не связаны с фазами предшествующих. В момент исчезновения цуга или возникновения нового фаза суммарной волны испытывает малые скачкообразные изменения, которые носят случайный (непредсказуемый) характер. Число таких случайных скачков фазы за некоторый промежуток времени пропорционально его длительности.

Временем когерентности t_k. будем называть время, в течение которого изменение фазы волны в рассматриваемой точке пространства, вследствие последовательности случайных малых ее изменений, может достигать значения π.

Используя данное определение время когерентности можно оценить из условия

,

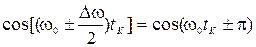т.е. ,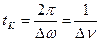

где Δn - ширина спектра по шкале частот.

Очевидно, что t_k равно длительности цуга τ. Если запаздывание Δt одной из двух волн, полученных от одного источника, в данной точке пространства, превысит τ, то в этой точке будут накладываться разные цуги (т. е. сопряженные цуги не перекрываются) и, следовательно, накладываемые волны окажутся некогерентными.

Расстояние, на которое перемещается волна за время когерентности, называется длиной когерентности или длиной цуга l_k. Очевидно, что для вакуума

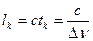
Так как 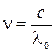, то, дифференцируя эту формулу, получим 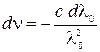. Следовательно, справедливо приближенное выражение 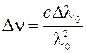. Поэтому имеем:

,

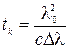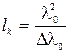. (4)

Условие существования интерференционной картины в виде Δt < τ можно переписать следующим образом

Δ_опт< l_k (5)

Здесь Δ_опт – оптическая разность хода,

l_k – длина когерентности.

Ртутные лампы низкого давления, обладающие невысокой интенсивностью, дают линии, для которых l_k составляет порядка нескольких миллиметров. Ртутные лампы высокого и сверхвысокого давления с высокой интенсивностью дают более низкое значение l_k (порядка нескольких десятых долей миллиметра). Примерно такое же значение l_k можно получить для квазимонохроматических световых волн, получаемых с помощью светофильтров из сплошного спектра ламп накаливания. Для излучения лазеров l_k значительно больше и может достигать нескольких километров.

Условие (5) позволяет оценить максимальное число порядков m_max, наблюдаемых при интерференции. Так как Δ_опт(max)=m_maxλ₀=l_k , то с учетом формулы (4) получим

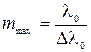
Под пространственной когерентностью понимают согласованность колебаний, которые совершаются в один и тот же момент времени, в различных точках плоскости, перпендикулярной направлению распространения света. Для реальных источников, имеющих конечную протяженность, эта согласованность нарушается вследствие следующих причин. Во-первых, колебания, созданные разными точками протяженного источника света в некоторой точке пространства складываются не в одной фазе из-за разности расстояний от них до данной точки. Во-вторых, две точки протяженного источника излучают тем менее согласованно (т.е. случайное изменение фазы между ними оказывается большим), чем больше расстояние между ними (даже в том случае, если расстояние от них до точки пространства, где производиться сложение колебаний, одинаково). Тем не менее, для плоскости, перпендикулярной направлению распространения света, можно указать размер области, называемый длиной или радиусом пространственной когерентности, колебания в пределах которой можно считать когерентными. Если в пределах этой области поместить две щели, они будут излучать когерентные волны и будет наблюдаться интерференционная картина.

Длиной или радиусом пространственной когерентности условились называть расстояние вдоль волновой поверхности (в направлении, перпендикулярном направлению распространения волны), на котором изменение фазы вследствие случайных малых ее изменений, достигает значения π.

Можно показать, что длина пространственной когерентности для источника света в виде светящегося диска приблизительно равна

l_п»l¤a,

где a - угловой размер источника.

Отсюда видно, что чем меньше угловой размер источника, тем больше длина пространственной когерентности, и для точечного источника света она равна бесконечности. Т.е. точечный источник является полностью пространственно когерентным