КОЛЕЦ НЬЮТОНА.

В данной лабораторной работе рассматривается применение интерференции света, одного из явлений, подтверждающих его волновую природу.

Явление наложения световых волн, в результате которого в одних точках пространства суммарная интенсивность света усиливается (max), а в других- ослабляется (min), называется интерференцией света. Наблюдаемую при этом картину чередующихся светлых и темных областей называют интерференционной картиной. Не все волны при наложении дают устойчивую интерференционную картину, а только те, разность фаз колебаний которых не зависит от времени. Такие волны называют когерентными (согласованными). Две световые волны будут когерентными, если они линейно поляризованы в одной плоскости, имеют одинаковую частоту и разность их начальных фаз не зависит от времени.

Волны, получаемые от независимых источников света, представляют собой суперпозицию волн, излучаемых отдельными атомами источников независимо друг от друга со случайными значениями фаз в момент начала и обрыва излучения. Поэтому они не будут когерентными. Для получения когерентных волн от естественного источника света используют прием разделения испускаемой им волны каким-либо способом (зеркала Френеля, бипризма Френеля, билинза Бийе и т.п.) на две и более волн. Вследствие общности происхождения эти волны будут когерентными.

Подобное разделение на две когерентные волны происходит и при падении света на пластинку, отличающуюся по своим оптическим свойствам от окружающей среды. При отражении падающей световой волны от верхней и нижней поверхностей пластинки получаются две когерентные волны. Чтобы в обеих волнах присутствовали излучения одинаковых атомов пластинка (пленка) должна быть тонкой. Поэтому явление интерференции в этом случае получило название интерференции света в тонких пленках.

Различают два вида интерференции в тонких пленках. В первом случае падающий на плоскопараллельную пластинку свет содержит волны с различной ориентацией волнового вектора (рассеянный свет). Получаемые в этом случае при интерференции линии максимумов и минимумов интенсивности от волн с одинаковым направлением распространения носят названий линий равного наклона. Они локализованы на бесконечности. Во втором случае плоская световая волна (параллельные лучи) падает на тонкую пленку переменной толщины. При этом на поверхности пленки видны темные и светлые интерференционные полосы. Эти полосы называют полосами равной толщины, так как каждая из них проходит через точки с одинаковыми значениями толщины пленки и локализованы они на поверхности или вблизи ее поверхности.

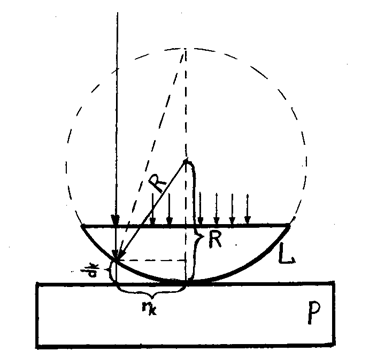
Частным случаем полос равной толщины являются кольца Ньютона. Кольца Ньютона наблюдаются в том случае, когда выпуклая поверхность линзы L (см. рис. 1.а), имеющая большой радиус кривизны R, соприкасается с плоской поверхностью хорошо отполированной пластинки Р. Между линзой и пластинкой образуется при этом воздушная прослойка, постепенно утолщающаяся от центра к периферии (воздушный клин). Если на линзу падает пучок монохроматического света, то световые волны, отраженные от верхней и нижней границ этого клина, будут когерентными и могут давать интерференционную картину. Результат интерференции накладывающихся волн зависит от разности фаз, которая определяется выражением:

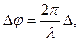(1)

где D - оптическая разность хода волн, l - длина волны света в вакууме.

Оптическая разность хода двух когерентных волн от одного источника, одна из которых проходит расстояние l₁ (длина пути) в среде с абсолютным показателем преломления n₁, а другая – l₂ в среде с абсолютным показателем преломления n₂, находится по формуле:

D = S₂ ¾ S_{1 ,}

где S₁=n₁l₁ и S₂=n₂l₂ - оптические длины путей соответствующих волн.

Если 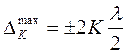, (2)

где К — любое целое число, K = 0, 1, 2, 3, то выполняется условие максимума (виден свет), если же

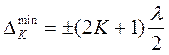, (3)

то выполняется условие минимума (свет не наблюдается).

В нашем случае точки поверхности клина, имеющие одинаковую толщину, лежат на окружностях, центры которых находятся на оси, проходящей через точку касания линзы с поверхностью отполированной пластинки. Поэтому интерференционная картина в отраженном свете будет иметь следующий вид: в центре линзы видно темное пятно (минимум нулевого порядка), окруженное системой чередующихся светлых и темных полос (колец) увеличивающихся радиусов, ширина и интенсивность которых постепенно убывают по мере удаления от центра (Рис. 1б).

Произведем расчет радиусов темных колец. Пусть лучи монохроматического света падают перпендикулярно пластинке, тогда геометрическая разность хода лучей, отраженных от верхней и нижней стороны воздушного клина будет равна: 2 d_K, где d_K - толщина зазора в данном месте клина. Кроме того, надо учесть, что при отражении от пластинки, представляющей оптически более плотную среду чем воздух, волна меняет свою фазу на p, что эквивалентно потере полуволны. На верхней же границе клина потери полуволны не происходит, так как там луч отражается от менее плотной среды — воздуха. Окончательное выражение для оптической разности хода D имеет вид:

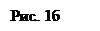
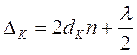. (4)

В этой формуле d_K - толщина клина в данном месте,
n - показатель преломления (в данном случае для воздуха n = 1),
l - длина волны падающего света.

Из геометрических соображений (рис.1.а) можно получить соотношение между толщиной воздушного зазора d_K, радиусом линзы R и радиусом соответствующего светлого кольца Ньютона:

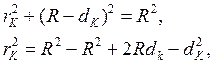
откуда, пренебрегая членом 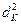, получим:

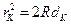, (5)

где R - радиус кривизны линзы, r_K - радиус "k"-го кольца, d_K - толщина клина в том месте, где наблюдается "k"-е кольцо (индекс соответствует номеру кольца).

Если наблюдать за темными кольцами, то в выражении для оптической разности хода (4) нужно подставить значение D из условий минимума (3), тогда:

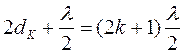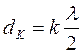или . (6)

Решая совместно (5) и (6), найдем, что кривизны радиус линзы и радиус "k"-го кольца (темного) связаны соотношением

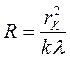. (7)

Более точные значения радиуса кривизны линзы получаются в случае, если определить радиусы нескольких колец Ньютона (например: 2-го, 4-го, 6-го), а потом сгруппировать их попарно. В этом случае формула для расчета среднего радиуса кривизны линзы примет вид:

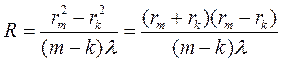(8)

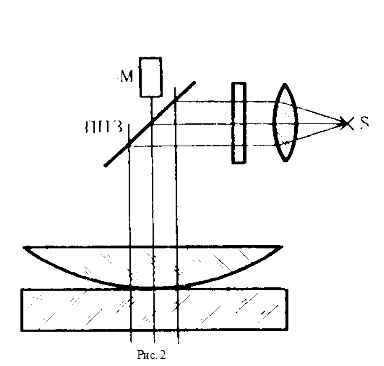
где "m" и "k" — номера колец (например: m=4, k=2 и т. п.). Схема установки, применяемой в данной работе, представлена на рис. 2. Можно предложить также графический метод расчета радиуса кривизны линзы, исходя из формулы (7).

Свет от источника с помощью полупрозрачного зеркала ППЗ, поставленного под углом 45° к падающим лучам, направляется на систему линза-стекло. Воздушный зазор между линзой и стеклянной пластинкой, как указывалось выше, образует клин при отражении от границ которого, лучи приобретают оптическую разность хода, зависящую от толщины зазора.