ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ С ПОМОЩЬЮ
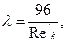
где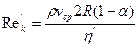 
- обобщенный параметр Рейнольдса, 
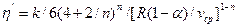— приведенная вязкость жидкости Освальда — Вейля для кольцевого канала.
В предельном случае, когда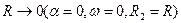 
, уравнение (3.43) не имеет смысла, а из зависимости (3.42) следует элементарная формула для распределения скорости в сечении круглой трубы
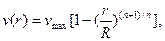
где
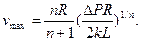
Поэтому основные интегральные характеристики потока жидкости в трубе принимают вид
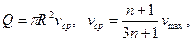
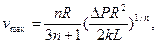
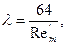
где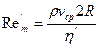 
— обобщенный параметр Рейнольдса и 
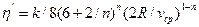— приведенная вязкость жидкости для трубы.
4. При турбулентном режиме течения, учитывая соотношения (3.1) и характер распределения профиля скорости [см., например, соотношение (3.41)], найдем по уравнениям Прандтля (2.20) связь напряжения Рейнольдса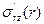 
с усредненной по времени скоростью 
:
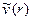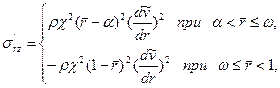(3.46)
Если исходить из тех же упрощающих предположений Прандтля, что и в области основного турбулентного ядра напряжения 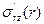, принять равными касательным напряжениям на стенках канала соответственно слева и справа от цилиндрической поверхности r = ωR, то, используя формулу (21) при r = αR и r = R, получим
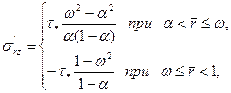(3.47)
где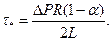 
Из сравнения соотношений (3.46) и (3.47) получим уравнение относительно скорости
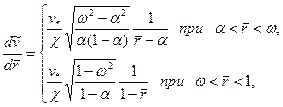
где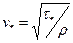 
- характерная скорость. Интегрируя данное уравнение с учетом условия 
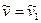при 
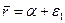и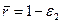 
, получим закон распределения скорости в кольцевом канале
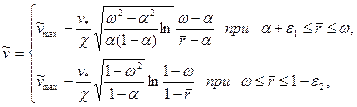(3.48)
где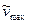 
— максимальная скорость потока:
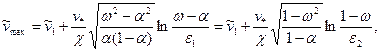(3.49)
содержит экспериментальные параметры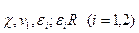 
— размеры пристенных слоев у внутренней и внешней стенок канала.
Из равенства (3.49) следует уравнение относительно параметра ω
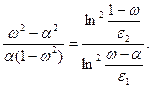(3.50)
Для упрощения решения этого трансцендентного уравнения примем, что отношения размеров зон турбулентного ядра и пристенных слоев слева и справа от поверхности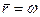 
равны между собой, т. е.
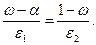(3.51)
Тогда из уравнения (3.50) получим
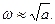(3.52)
Путем интегрирования профиля скорости (3.48), пренебрегая пристенными слоями и используя равенство (3.52), легко найти среднюю скорость турбулентного потока
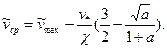(3.53)
Согласно формуле (3.5) коэффициент сопротивления
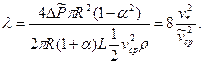
Отсюда, учитывая формулы (3.49), (3.52) и (3.53), получим
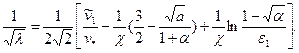
Принимая по аналогии с задачей для гладких стенок: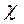 
= 0,4; 
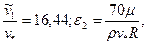закон сопротивления для кольцевого канала запишем в виде
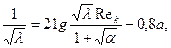(3.54)
где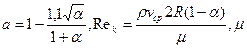 
- вязкость или приведенная вязкость жидкости.
Рис. 25. Зависимость коэффициента сопротивления от параметра Рейнольдса (закон сопротивления) при турбулентном режиме течения:
1, 2 – соответственно при α = 0,9 и α = 0.
Если α = 0, то а=1 и соотношение (3.54) выражает известный универсальный закон сопротивления Прандтля для гладких труб, который неоднократно был проверен опытами.
При α > 0,3 величина а изменяется в пределах от 0,54 до 0,45. Следовательно, для малых кольцевых зазоров (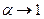 
) закон сопротивления (3.54) принимает вид закона сопротивления для щели (3.28), где 2h = R( 1 - α).
Из рис. 25 следует вывод, что закон сопротивления при турбулентном режиме течения слабо зависит от α, т. е. от формы канала (круглая труба, кольцевое пространство или щель). В диапазоне чисел Рейнольдса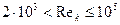 
кривые на рис. 25 можно аппроксимировать функцией 
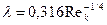, которую принято называть формулой Блазиуса.
Таблица 2.
| S0/R | а | ||||
| 0,3 | 0,5 | 0.7 | 0,9 | ||
| 0,001 | 0,016 | 0,018 | 0,02 | 0,023 | 0,032 |
| 0,005 | 0,025 | 0,027 | 0,031 | 0,037 | 0,056 |
| 0,01 | 0,03 | 0,034 | 0,038 | 0,047 | 0,077 |
| 0,025 | 0,041 | 0,046 | 0,054 | 0,069 | — |
| 0,05 | 0,053 | 0,062 | 0,073 | — |
Отсюда непосредственно находят коэффициент сопротивления по высоте элемента шероховатости s0 стенки канала. Некоторые значения λ, вычисленные по этой формуле, приведены в табл. 2.
Полученные выше решения дают основание сделать следующий практический вывод: при гидравлических расчетах или обработке опытных данных кольцевой канал скважины можно рассматривать как щель с параметрами 2h = R( 1 - α) и b =π R( 1 + α). При этом точность расчета будет зависеть в основном от точности значений реологических параметров жидкости и геометрических параметров кольцевого зазора.
Для расчета гидравлических потерь при турбулентном режиме течения жидкости в затрубном пространстве открытой части ствола скважины необходимо воспользоваться формулой Дарси — Вейсбаха, в которой среднестатистическое значение коэффициента λ должно быть установлено по опытным данным в п типовых скважинах.
ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ С ПОМОЩЬЮ
Дата добавления: 2015-03-07; просмотров: 751;