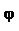ДИФРАКЦИОННОЙ РЕШЕТКИ.

Согласно законам геометрической оптики свет в однородной среде распространяется прямолинейно. Следствием этого должно быть образование четко ограниченной тени за непрозрачным предметом при падении на него света. Реально, когда световая волна проходит вблизи краев экранов, отверстий или иных неоднородностей, фронт ее искажается, вследствие чего световые лучи отклоняются от прямой и проникают в область тени. Свет как бы огибает препятствие. Особенно ярко это проявляется, если размеры препятствия сравнимы с длиной падающей световой волны. Тень за таким препятствием приобретает сложный характер. Такое явление отклонения от законов прямолинейного распространения света при прохождении его вблизи краев отверстий, экранов и других неоднородностей среды называется дифракцией света.

Явление дифракции света получает простое объяснение с точки зрения волновой теории и является, таким образом, доказательством его волновой природы. Описать это явление можно, используя принцип Гюйгенса-Френеля.

Принцип Гюйгенса: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих вторичных волн дает положение фронта первичной волны в следующий момент времени.

Принцип Гюйгенса не дает никаких указаний об интенсивности волн. Этот недостаток был устранен Френелем, который дополнил его положением о интерференции вторичных волн.

Принцип Гюйгенса – Френеля:каждый элемент волновой поверхности служит источником вторичной сферической волны, амплитуда которой пропорциональна величине поверхности элемента dS. Интерференция вторичных волн в рассматриваемой точке дает амплитуду и фазу колебаний первичной волны в этой точке.

Таким образом, согласно Френелю вторичные волны интерферируют между собой, вследствие чего образуется фронт распространяющейся волны.

Для упрощения решения задачи об интерференции вторичных волн Френель предложил разбивать волновую поверхность на зоны, являющиеся вторичными источниками, такие, чтобы разность хода волн, приходящих от границ двух соседних зон, отличалась на l/2. Их называют зонами Френеля. При таком разбиении волновой поверхности разность фаз колебаний волн, приходящих в рассматриваемую точку от двух соседних зон Френеля, будет отличаться на p, тоесть складываясь, волны от этих зон будут вычитаться.

Рассмотрим дифракцию света на щели. Щель — узкая, бесконечно длинная, шириной a . Плоская монохроматическая световая волна падает нормально на плоскость, в которой расположена щель (рис. 1). Параллельно расположена линза L, в фокальной плоскости которой, находится экран Э. Согласно принципу Гюйгенса - Френеля каждая точка волновой поверхности, попавшей в щель, становится источником вторичных волн, которые дают лучи всевозможных направлений. Лучи, идущие от всех точек щели под одинаковыми углами, собираются в одной точке экрана, где и интерферируют между собой.

В зависимости от угла наблюдения j поверхность разбивается на разное число зон Френеля (определение зон Френеля смотри в Савельев И.В. Курс общей физики, М., Наука, 1988, т.2, §§ 127,128,129) . Выражение

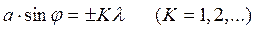(1а)

является условием минимумов интенсивности, где j - угол наблюдения, l - длина световой волны. Это выражение легко получить из следующих соображений. Если разность хода D лучей от краев щели до точки наложения на экране равна ±Kl, открытую щелью часть волновой поверхности можно разбить на 2K равных по ширине зон, причем разность хода от краев каждой зоны до точки наложения на экране будет равна l/2. Колебания от каждой пары соседних зон взаимно погашают друг друга, так что результирующая амплитуда равна нулю. Если для точки наложения волн на экране разность хода волн от краев щели D равно ±(K+1/2)l, то число зон уместившихся в размер щели будет нечетным, действие одной из них окажется некомпенсированным, и будет наблюдаться максимум интенсивности

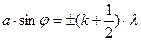(К=1,2,…) (1б)

Интенсивность света пропорциональна квадрату амплитуды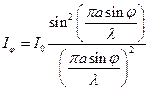

где I₀ – интенсивность в середине дифракционной картины против центра линзы (всегда max), I_j - интенсивность в точке, положение которой определяется данным значением j.

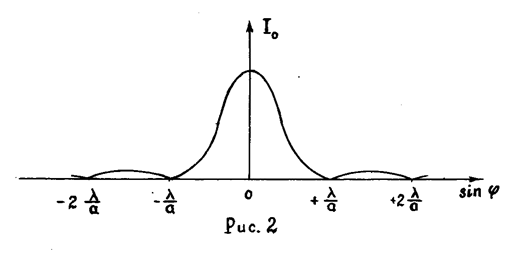
График зависимости интенсивности I_j от Sinj представлен на рис. 2.

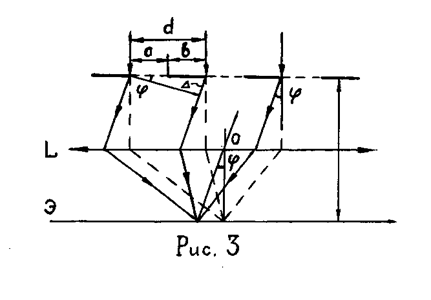
Рассмотрим теперь совокупность N одинаковых щелей шириной а, расположенных на одинаковом расстоянии b друг от друга. Такая совокупность образует периодическую структуру, называемую дифракционной решеткой. Период решетки d = a + b. Как и в случае одной щели плоская монохроматическая волна падает перпендикулярно плоскости, в которой расположена дифракционная решетка. Световые волны от каждой из щелей собираются линзой L на экране Э, расположенном в фокальной плоскости линзы (рис. 3).

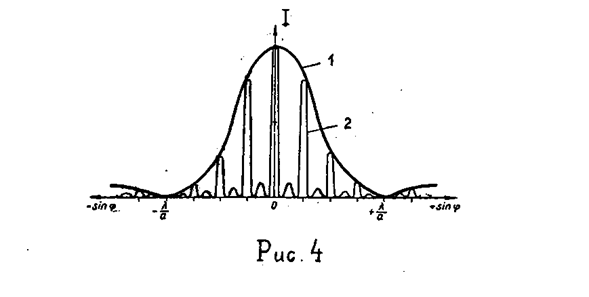
Если бы световые волны в каждой из щелей были некогерентными, то картина дифракции в этом случае была подобна картине, наблюдаемой в случае одной щели (кривая 1 рис. 4), только интенсивность возросла бы в N раз (N— число щелей). Вследствие когерентности этих волн (световая волна в каждой из щелей является участком фронта падающей световой волны) при их сложении интенсивность возрастает в N² раз, и на картине распределения интенсивности, наблюдаемой при дифракции света на одной щели, вследствие интерференции, появятся дополнительные максимумы и минимумы. Зависимость интенсивности I от Sinj в этом случае для N =3 представлена на рис.4 (кривая 2). На этой зависимости можно видеть главные и дополнительные максимумы, отличающиеся своей интенсивностью. Между главными максимумами расположено (N–1) дополнительных минимумов. Вследствие малой интенсивности дополнительные максимумы, как правило, человеческим глазом не воспринимаются, и мы видим только главные максимумы дифракционной картины. Таким образом, вследствие дифракции на дифракционной решетке световая волна после нее распространяется в основном по направлениям, соответствующим главным максимумам.

Условия главных максимумов получим из следующих соображений. Результат интерференции световых волн зависит от их оптической разности хода. В соответствии с рис. 3 оптическая разность хода волн, идущих от двух соседних щелей под углом j равна:

D = d×Sinj . (2)

Показатель преломления среды в этой формуле положен равным 1.

Тогда максимум интенсивности при интерференции волн от щелей будет иметь место, если

d×Sinj = ±K×l . (2а)

Здесь j - угол дифракции, l - длина падающей световой волны, К - порядок максимума (К = 0; 1; 2;...).

Это и есть условие наблюдения главных максимумов при дифракции света на дифракционной решетке. Таким образом, на экране мы получим максимум нулевого порядка, соответствующий условию K = 0 и обладающий наибольшей интенсивностью. Симметрично от него расположатся максимумы 1-ого, 2-ого и т.д. порядков (кривая 2 рис. 4) интенсивность которых постепенно убывает.

Если падающая на дифракционную решетку световая волна не монохроматическая, а имеет сложный состав (естественный свет), то получаемая в этом случае дифракционная картина имеет более сложный характер. При K = 0, то есть в направлении падающего света, условие максимума удовлетворяется для всех l, поэтому в этом случае получается центральная светлая полоса, цвет которой определяется спектральным составом падающего света. Для всех остальных значений k светлые полосы каждого цвета (то есть максимумы для разных длин волн) наблюдаются раздельно. В результате на экране возникнет ряд цветных полос, образующих спектры, расположенные по обе стороны от центрального изображения щели (нулевой порядок спектра). Чем больше длина волны, тем больше согласно (2а) и дифракционный угол.

Предельное число максимумов k, которое можно получить при помощи решетки для каждой длины волны, дается соотношением:

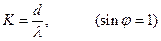
Так как диапазон видимых световых длин волн велик (приблизительно от 0,4 микрон до 0,7 микрон), то может наблюдаться наложение спектров разных порядков друг на друга.