Определение разрешающей способности решетки.

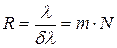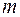Разрешающая способность решетки равна: , где – порядок спектра, N- число штрихов решетки. Для того, чтобы оценить разрешающую способность решетки, нужно взять источник света, спектр которого богат близко расположенными линиями и определить, какая пара линий в этом спектре представляется как одна линия независимо от геометрического увеличения окулярного устройства. Зная длину решетки (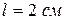 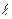), найти число штрихов N и вычислить

Задание 4. Экспериментальное изучение явления дифракции Фраунгофера на разных объектах: одной или несколько щелях и проволоке.

Дифракция на проволоке. Для нахождения дифракционной картины от проволоки толщиной 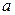проведем следующие рассуждения. При расчете дифракционной картины от щели той же ширины 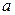мы искали суммарный вклад от вторичных источников, расположенных на открытой части исследуемого объекта. Для проволоки, наоборот, данная часть объекта будет закрытой, а остальное пространство открытым. Такие объекты, как бы дополняющие друг друга, носят название дополнительных.

Обозначим распределение светового поля на экране в случае дифракции на щели 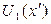, а на проволок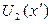е , где 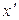- координата в плоскости экрана. Тогда сумму полей 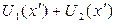можно представить как сумму интегралов по открытым областям для каждого из этих объектов, или как интеграл от суммы открытых областей. Но отверстия для дополнительных объектов располагаются так, что полностью «открывают» весь волновой фронт падающего излучения, следовательно: 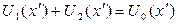, где 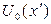- волновое возмущение на экране в случае отсутствия какого-либо препятствия. Таким образом, сумма распределения полей от дополнительных объектов равна полю, наблюдаемому при отсутствии препятствия. Полученный результат носит название принципа Бабине.

Если в качестве источника плоской волны используется лазер, размеры пучка которого много больше ширины щели 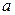, то на экране в случае отсутствия препятствия будет наблюдаться яркое пятно, а в остальной области экрана поле можно считать равным нулю. Для этой «незасвеченной» области справедливо выражение: 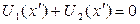,следовательно 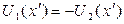, а для интенсивностей: 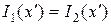. В области основного пятна 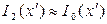, так как в данной области .

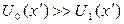Таким образом, для дополнительных объектов – щели и проволоки одинаковых размеров, распределение интенсивности на экране одинаково всюду, за исключением области, куда попадает исходный пучок в случае отсутствия препятствия. Если толщина проволоки такова, что размер первого дифракционного максимума для щели такой же ширины, как и проволока, превысит размер пучка лазера, то для обоих объектов будут совпадать координаты как всех минимумов, так и всех максимумов дифракционной картины.

Обратим внимание на одно интересное явление. Иногда при дифракции на проволоке, кроме минимумов, соответствующих дифракционным минимумам, наблюдаемым при дифракции на щели того же размера, можно заметить еще два резких глубоких минимума в тех областях, где сильно уменьшается интенсивность лазерного пучка. Это явление легко объяснить, исходя из принципа Бабине. В самом деле, в области лазерного пучка справедливо соотношение 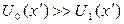, а в той области, куда лазерное излучение не попадает, 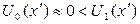. Следовательно, существует такая точка 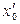, в которой 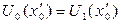, и, следовательно, 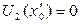. Эта точка находится на границе лазерного пучка, а так как интенсивность пучка в этой области обычно падает достаточно резко, то «провал» в интенсивности имеет малую ширину. Так как размеры окна фотодиода, используемого в установке, сравнимы с размером «провала», при регистрации дифракции на проволоке уменьшение интенсивности регистрируется не всегда.