Дифракция Фраунгофера на дифракционной решетке

Дифракционная решетка - оптический прибор, представляющий собой совокупность большого числа параллельных, равноотстоящих друг от друга узких щелей (штрихов) одинаковой формы, нанесенных на какую-либо поверхность. Основное свойство дифрак­ционной решетки - способность раскладывать падающий на нее свет в спектр по длинам волн. Различают отражательные и прозрачные дифракционные решетки. У отражательных штрихи наносятся на зеркальную (как правило, металлическую) поверхность, наблюдение спектра ведется в отраженном свете. У прозрачных решеток штрихи наносятся на поверх­ность прозрачной (как правило, стеклянной) пластины либо вырезаются в виде узких ще­лей в непрозрачном экране и наблюдение ведется в проходящем свете.

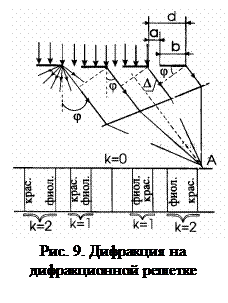Пусть на решетку нормально к ее по­верхности падет параллельный пучок белого света (рис. 9). На щелях (штрихах) решетки, соизмеримых с длиной волны света, происходит явление дифракции, определенное как отклонение волн от прямолинейного распространения при взаимодействии их с препятст­вием. В результате за решеткой лучи пойдут под раз­ными углами во все стороны от каждой точки щели. Эти лучи можно сгруппировать в пучки параллельных между собой лучей. Установим за решеткой положи­тельную линзу. Каждый пучок параллельных лучей соберется в задней фокальной плоскости линзы в од­ной точке (точка А для лучей, дифрагировавших под углом φ к нормали решетки). Параллельные лучи других углов дифракции линза собирает в других точках фокальной плоскости. В этих точках произойдет интерференция световых волн, исходящих от разных щелей решетки. Если в разности хода между соответствующими лучами укладывается целое число длин волн монохроматического света, то в точке встречи лучей возникает максимум интенсив­ности света для данной длины волны, то есть, Δ = kλ, k = 0,±1,±2,....

Из рис. 9 видно, что разность хода Δ между двумя параллельными лучами, выходя­щими из соответствующих точек соседних щелей, равна Δ = (а + b) sin φ = d sin φ, где а -ширина щели; b - ширина непрозрачного промежутка между щелями. Величина d = а + b называется периодом, или постоянной, дифракционной решетки. Следовательно, условие возникновения главных интерференционных максимумов решет­ки имеет вид

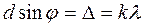
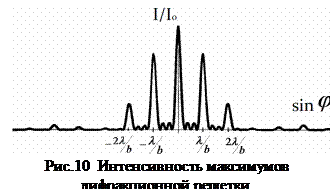Входящая в формулу величина k носит название порядка спектра. В фокальной плоскости линзы для лучей, не испытавших дифракции, наблюдается центральный белый максимум нулевого порядка (φ= 0, k = 0), вправо и влево от которого располагаются цветные максимумы (спектральные линии) первого, второго и последую­щих порядков интерференции (рис. 9). Интенсивность максимумов сильно уменьшает­ся с ростом их порядка, то есть с увеличением угла дифракции (рис.10)

Уравнение главных интерференционных максимумов позволяет рассчитать период дифракционной решетки d, если измерен угол дифракции φ, соответствующий спектральной линии, для которой известны ее длина волны и порядок спектра.

При k=0 условие максимума удовлетворяется для всех длин волн, то есть при k=0 наблюдается центральная светлая полоса Знак (+) или (-) для всех остальных значений соответствует двум системам спектра, расположенных симметрично справа и слева от центральной световой полосы.

Как следует из равенства, углы, при которых наблюдаются световые максимумы, зависят от длины волны . Дифракционная решетка представляет собой, таким образом, спектральный прибор. Если на дифракционную решетку падает свет сложного спектрального состава, то после решетки образуется спектр, причем фиолетовые лучи отклоняются решеткой меньше, чем красные.