Дифракция на круглом отверстии.
Вид дифракционной картины в точке Р зависит от числа зон Френеля, укладывающихся в отверстии.
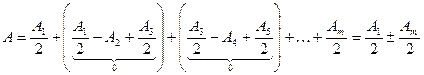
знак плюс соответствует нечетным m и минус — четным m.
Дифракционная картина вблизи точки Р будет иметь вид чередующихся темных и светлых колец с центрами в точке Р. Если m четное, то в центре будет темное кольцо, если m нечетное — то светлое кольцо.
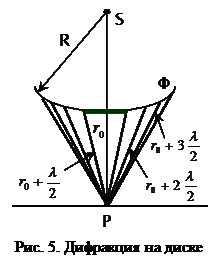
Дифракция на диске.
В данном случае зоны Френеля надо строить начиная с краев диска. Пусть диск закрывает m первых зон Френеля.
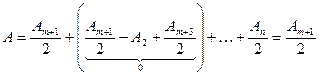
В центре всегда наблюдается интерференционный максимум - т.н. пятно Пуассона, окруженный концентрическими с ним темными и светлыми кольцами. Диаметр и яркость пятна увеличиваются при уменьшении диаметра диска.
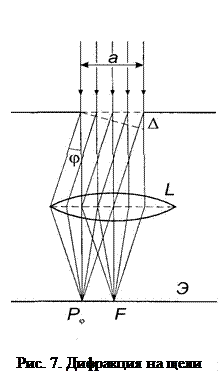Дифракция от одной щели. Дифракцию плоских световых волн, или дифракцию в параллельных лучах, рассмотрел немецкий физик И. Фраунгофер. Чтобы этот тип дифракции осуществить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы (L на рис.7), установленной за препятствием.
Пусть плоская монохроматическая световая волна падает нормально на щель шириной а (а ≈λ), длина которой значительно больше ее ширины (рис. 7).
Щель становится центром вторичных волн,волны распространяются по всем направлениям, волна становится цилиндрической. Так как плоскость щели совпадает с фронтом падающей волны, то точки щели колеблются в одной фазе.
Оптическая разность хода между крайними лучами, идущими от щели в произвольном направлении φ равна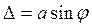 
,
Разобьем открытую часть волновой поверхности в плоскости щели а на зоны Френеля, имеющие вид полос, параллельных ребру щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна λ/2, т. е. всего на ширине щели уместится N зон: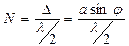 
, т.е. число зон Френеля, укладывающихся на ширине щели, зависит от угла φ.
От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн: при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно погашают друг друга.
Следовательно, если число зон Френеля четное
а sin j = ± 2m l /2, (m= 1, 2, 3, ...),
то в точке Рφ наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное
а sin j = ± (2m + 1) l / 2 (m=l, 2, 3, ...),
то наблюдается дифракционный максимум, соответствующий действию одной скомпенсированной зоны Френеля. Величина m, принимающая значения чисел натурального ряда, называется порядком дифракционного максимума. Знаки ± в формулах соответствуют лучам света, дифрагирующим от щели под углами +j и -j и собирающимся в побочных фокусах линзы L. В направлении j = 0 наблюдается самый интенсивный центральный максимум нулевого порядка.
Положение максимумов дифракции по формуле соответствует углам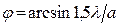 
, 
, 
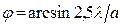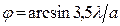и т.д.
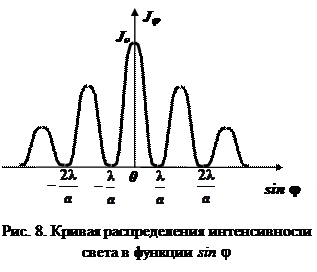На рис.8 приведена кривая распределения интенсивности света в функции sin j. Положение центрального максимума (j = 0) не зависит от длины волны и, следовательно, является общим для всех длин волн. Поэтому в случае белого света центр дифракционной картины представится в виде белой полоски. Ясно, что положение максимумов и минимумов зависит от длины волны. Поэтому простое чередование темных и светлых полос имеет место только при монохроматическом свете. В случае белого света дифракционные картины для волн с разными l сдвигаются в соответствии с длиной волны. Центральный максимум белого цвета имеет радужную окраску только по краям (на ширине щели укладывается одна зона Френеля). Боковые максимумы для разных длин волн уже не совпадают между собой; ближе к центру располагаются максимумы, соответствующие более коротким волнам. Длинноволновые максимумы отстоят друг от друга дальше (j =arcsinl/2), чем коротковолновые. Поэтому дифракционный максимум представляет собой спектр, обращенный к центру фиолетовой частью.
Дата добавления: 2015-02-25; просмотров: 1932;