Интерполяционный полином Ньютона.

Ньютон предложил следующий вид интерполяционного полинома:

Коэффициенты этого полинома A₀, A₁, A₂,...,A_n определяются из условий Лагранжа (5.3).

Полагаем x=x₀. Тогда в (5.6) все слагаемые, кроме A₀, обращаются в нуль, следова­тель­но,

A₀ = f₀.

Затем полагаем x=x₁, тогда из (5.3) имеем:

f₀ + A₁(x₁-x₀)= f₁,

откуда находим коэффициент A₁:

A₁ = или A₁ = f₀₁.

Величина f₀₁ = называется разделенной разностью первого порядка. При малом расстоянии между x₀ и x₁ эта величина близка к первой производной от функции f(x), вычисленной в точке x=x₀.

При x=x₂ полином (5.6) принимает вид:

P_n(x)= f₀+f₀₁(x-x₀)+A₂(x-x₀)(x-x₁) ,

откуда с учетом (5.3) получаем:

f₂ = f₀+f₀₁(x₂-x₀)+A₂(x₂-x₀)(x₂-x₁) или f₂ -f₀-f₀₁(x₂-x₀) = A₂(x₂-x₀)(x₂-x₁) ,

следовательно, коэффициент A₂:

A₂= = = = ,

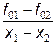где 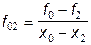. Обозначая 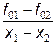= f₀₁₂ (разделенная разность второго порядка),

окончательно получаем выражение для A₂:

A₂ = f₀₁₂ .

Аналогично, при x=x₃, находим коэффициент A₃:

,

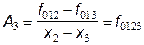где ; .

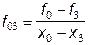Методом математической индукции можно получить для любого A_k (k=0,...,n) следующее выражение:

.

Полученные результаты сведены в представленной ниже таблице.

Следует отметить, что добавление новых узлов в исходных данных не изменяет уже вычисленные коэффициенты; таблица будет лишь дополняться новыми строками и столбцами.

В интерполяционный полином Ньютона входят только диа­го­нальные элементы данной таблицы, а остальные являются промежуточными данными. Для вычисления любого элемента этой таблицы необходимы: диагональный элемент предыдущего столбца и предыдущий элемент данной строки.

Поэтому в программе, реализующей данный алгоритм, не нужно организовывать двумерный массив. Более того, все разделенные разности, в том числе и диагональные элементы (коэффициенты полинома) можно помещать по мере вычисления на место исходных значений f_k. Следовательно, в программе можно ограничиться только двумя массивами: Х-для узлов и F-для значений аппроксимируемой функции. Массив F по мере выполнения программы будет заполняться разделенными разностями, и в конце концов в нем будут получены коэф­фициенты полинома A₀,A₁,A₂,... ,A_n.

Таким образом, данный метод аппроксимации, так же как и в случае канонического полинома, дает в качестве результата коэффициенты интерполяционного полинома.

После определения коэффициентов A₀,A₁,A₂,... ,A_n вычисление значений полинома Ньютона при конкретных аргументах x рекомендуется выполнять также по схеме Горнера, для чего полином (5.8) надо преобразовать к виду:

P_n(x)=A₀+(x-x₀)(A₁+(x-x₁)(A₂+...+(x-x_n-1)A_n)...)).

На рис.5.4 представлена блок-схема вычисления коэффициентов полинома Ньютона и его значений в точках интерполяции по схеме Горнера.

		Разделенные разности
x	f
x0	f0	=A0
x1	f1	f01=	=A1
x2	f2	f02=	f012=	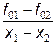=A2
x3	f3	f03=	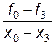f013=	f0123=	=A3
x4	f4	f04=	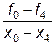f014=	f0124=	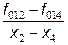f01234=	=A4