Выбор образующего полинома

Рассмотрим вопрос выбора образующего полинома, который определяет корректирующие свойства циклического кода. В теории циклических кодов показано, что образующий полином представляет собой произведение так называемых минимальных многочленов m_i(x), являющихся простыми сомножителями (то есть делящимся без остатка лишь на себя и на 1) бинома xⁿ+ 1:

P(x)=m₁(x)* m₃(x)…m_j(x), (*)

где j = d₀ – 2 =( 2t_u.ош+1) – 2 = 2 t_и.ош – 1.

Существуют специальные таблицы минимальных многочленов, одна из которых приведена ниже. Кроме образующего полинома необходимо найти и количество проверочных разрядов r. Оно определяется из следующего свойства циклических кодов:

для любых значений l и t_и.ош существует циклический код длины n =2^l – 1, исправляющий все ошибки кратности t_и.ош и менее, и содержащий не более 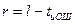проверочных элементов.

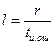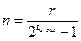Так как , то откуда . (**)

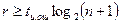Очевидно, что для уменьшения времени передачи кодовых комбинаций, r следует выбирать как можно меньше. Пусть, например, длина кодовых комбинаций n = 7, кратность исправляемых ошибок t_и.ош =1. Из (**) получим r = 1 ^. log₂ ( 7+1 )=3.

После определения количества проверочных разрядов r, вычисления образующего полинома удобно осуществить, пользуясь таблицей минимальных многочленов, представленной в следующем виде:

Таблица минимальных многочленов

J=2tи.ош -1	Вид минимальных многочленов для
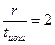
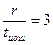
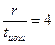
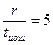
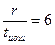
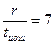
	x2+x+1	x3+x+1	x4+x+1	x5+x+1	x6+x+1	x7+x+1
	-	-	x4+x3+x2+x+1	x5+x4+x3+x2+1	x6+x4+x2+x+1	x7+x3+x2+x+1
	-	-	-	x5+x4+x2+x+1	x6+x5+x2+x+1	x7+x4+x3+x2+1
	-	-	-	-	x6+x3+1	X7+x6+x5+x4+x2+x+1

Определяя образующий полином, нужно из столбца для соответствующего соотношения 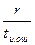выписать все многочлены, начиная с верхней строки до нижней с номером j=2t_и.ош–1 включительно. После этого следует перемножить выбранные минимальные многочлены в соответствии с (*). В частности, если r=3, t_и.ош=1, j=2*1-1=1, образующий полином будет представлять собой единственный минимальный многочлен P(x)= m₁(x) = x³+x+1 (первая строка, второй столбец таблицы ). Соответственно образующее число равно 1011.

УПС - обеспечивают согласование параметров сигналов источника с параметрами канала связи.

Согласование может производиться по:

– полосе частот;
– уровню;
– скорости.

Согласование спектра может производиться двумя путями:

· Перекодированием.

· С использованием несущей (модуляции).

Известно, что спектр последовательности прямоугольных импульсов имеет вид (sin x)/x с максимумом на нулевой частоте. Основная энергия сигналов в этом случае сосредоточена в полосе частот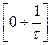

Канал связи, из-за наличия развязывающих трансформаторов, не пропускает постоянную составляющую. Из-за этого однополярные сигналы будут испытывать значительные искажение.