Понятие о корректирующих кодах
Пусть имеется источник сообщений с объемом алфавита К.
Поставим в соответствие каждому сообщению n - элементную двоичную последовательность. Всего последовательностей из n - элементов может быть 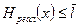 .
.
Если 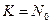 , то все последовательности (или кодовые комбинации) будут использоваться для кодирования сообщений, т.е. будут разрешенными.
, то все последовательности (или кодовые комбинации) будут использоваться для кодирования сообщений, т.е. будут разрешенными.
Полученный таким образом код называется простым, он не способен обнаруживать и исправлять ошибки.
Для того, что бы код мог обнаруживать и исправлять ошибки необходимо выполнение условия 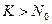 , при этом неиспользуемые для передачи комбинации (N0-K) называют запрещенными.
, при этом неиспользуемые для передачи комбинации (N0-K) называют запрещенными.
Появление ошибки в кодовой комбинации будет обнаружено, если передаваемая разрешенная комбинация перейдет в одну из запрещенных.
Расстояние Хемминга – характеризует степень различия кодовых комбинаций и определяется числом несовпадающих в них разрядов.
Перебрав все возможные пары разрешенных комбинаций рассматриваемого кода можно найти минимальное расстояние Хемминга d0.
Минимальное расстояние d0 - называется кодовым расстоянием
Кодовое расстояние определяет способность кода обнаруживать и исправлять ошибки.
У простого кода d0=1 – он не обнаруживает и не исправляет ошибки. Так как любая ошибка переводит одну разрешенную комбинацию в другую.
В общем случае справедливы следующие соотношения
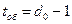 – для обнаруживающей способности
– для обнаруживающей способности
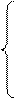
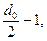 для четных
для четных
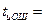
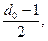 для нечетных
для нечетных
– для исправляющей способности
Линейные коды.
Двоичный блочный код является линейным если сумма по модулю 2 двух кодовых слов является также кодовым словом.
Линейные коды также называют групповыми.
Введем понятия группы.
Множество элементов с определенной на нем групповой операцией называется группой, если выполняется следующие условия:
1. Замкнутость gi 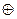 g j= gk
g j= gk 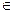 G в результате операции с двумя элементами группы получается третий, так же принадлежащий этой группе.
G в результате операции с двумя элементами группы получается третий, так же принадлежащий этой группе.
2. Ассоциативность (сочетательность) (gi 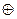 gj)
gj) 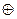 gk = gi
gk = gi 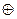 (gj
(gj 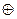 gk)
gk)
3. Наличие нейтрального элемента gj 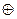 e = gj
e = gj
4. Наличие обратного элемента. gi 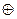 (gi)-1= e
(gi)-1= e
Если выполняется условие gi  gj = gj
gj = gj  gi, то группа называется коммутативной.
gi, то группа называется коммутативной.
Множество кодовых комбинаций n-элементного кода является замкнутой группой с заданной групповой операцией сложение по модулю 2.
Поэтому используя свойство замкнутости относительно операции  2, множество всех элементов можно задать не перечислением всех элементов, а производящей матрицей.
2, множество всех элементов можно задать не перечислением всех элементов, а производящей матрицей.
Все остальные элементы, кроме 0, могут быть получены путем сложения по модулю 2 строк производящей матрицы в различных сочетаниях.
В общем случае строки производящей матрицы могут быть любыми линейно независимыми, но проще и удобнее брать в качестве производящей матрицы – единичную.
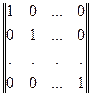
Дата добавления: 2015-01-26; просмотров: 1207;
