Расширенный дискретный канал

(Включает ДК+ Кодер + Декодер канала.)

Алфавит канала состоит из 2ⁿ сообщений, где n – число элементов в кодовой комбинаций

Характеризуется:

Коэффициентом ошибок по кодовым комбинациям

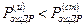(1.15)

Эффективной скоростью передачи информации – эффективная скорость учитывает, что не все элементы несут информацию и не все комбинации, поступающие на вход, выдаются получателю.

Так как РДК=КПД=ДК+УЗО, то основная задача решается на уровне РДК повышения верности передачи.

Методы повышения верности:

1. Меры эксплуатационного и профилактического характера

· повышения стабильности работы генераторного оборудования

· резервирование электропитания

· выявление и замена отказавшего оборудования

· повышение квалификации обслуживающего персонала

2. Мероприятия по увеличению помехоустойчивости передачи единичных элементов

· увеличение отношения сигнал – помеха (увеличение амплитуды, длительности…)

· применение более помехоустойчивых методов модуляции

· совершенствование методов обработки

· выбор оптимальных сигналов

однако это не всегда возможно!

3. Введение избыточности в передаваемую последовательность т.е. помехоустойчивое кодирование

Оценка требуемой исправляющей способности кода для обеспечения заданной верности приема блока

Положим что вероятность ошибки двоичного элемента в ДК 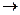P_ош.

Сообщения источника требуется передавать блоками по n-двоичных символов.

Требуется обеспечить вероятность неправильного приема блока не более некоторой заданной величины .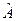

Рассмотрим все возможные ситуации при приеме последовательности из n – элементов.

1. вероятность правильного приема блока (1-P_ош)ⁿ;

2. вероятность ошибки кратности t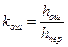

Совокупность всех возможных исходов будет составлять полную группу событий. Поэтому можно записать:

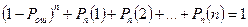(1.16)

при этом: 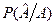- это вероятность того, что в блоке будет хотя бы одна ошибка. Другими словами – это есть P_НП– если не предпринято никаких мер защиты.

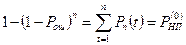(1.17)

Если 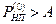, то необходимо обеспечить исправления ошибок некоторой кратности в блоке.

Оценим, ошибки какой кратности нужно исправить.

Найдем вероятность неправильного приема при исправлении однократной ошибки. Она будет равна:

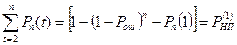. (1.18)

Вновь проводим сравним Р_н.п⁽¹⁾ и А, если требования не выполнилось, то убираем 2^х, 3^х и т.д. кратной ошибки.

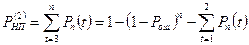(1.19)

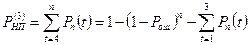(1.20)

Последняя кратность ошибки, вычитание вероятности которой привело к выполнению условия и будет требуемой исправляющей способностью кода.

При этом из всех n-элементов блока, часть (r) необходимо будет отдать на проверочные элементы, что естественно внесет избыточность в передаваемое сообщение и понизит скорость передачи

Эффективное кодирование – это процедуры направленные на устранение избыточности.

Основная задача эффективного кодирования – обеспечить, в среднем, минимальное число двоичных элементов на передачу сообщения источника. В этом случае, при заданной скорости модуляции обеспечивается передача максимального числа сообщений, а значит максимальная скорости передачи информации.

Пусть имеется источник дискретных сообщений, алфавит которого .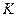

При кодировании сообщений данного источника двоичным, равномерным кодом, потребуется 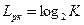двоичных элементов на кодирование каждого сообщения.

Если вероятности 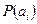появления всех сообщений источника равны, то энтропия источника (или среднее количество информации в одном сообщении) максимальна и равна:

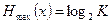(1.21)

В данном случае каждое сообщение источника имеет информационную емкость 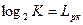бит, и очевидно, что для его кодирования (перевозки) требуется двоичная комбинация не менее 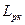элементов. Каждый двоичный элемент, в этом случае, будет переносить 1 бит информации.

Если при том же объеме алфавита сообщения не равновероятны, то, как известно, энтропия источника будет меньше:

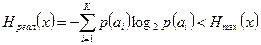(1.22)

Если и в этом случае использовать для перевозки сообщения 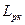- разрядные кодовые комбинации, то на каждый двоичный элемент кодовой комбинации будет приходиться меньше чем 1 бит.

Появляется избыточность, которая может быть определена по следующей формуле:

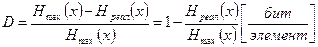(1.23)

Среднее количество информации, приходящееся на один двоичный элемент комбинации при кодировании равномерным кодом

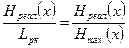(1.24)

Пример

Для кодирования 32 букв русского алфавита, при условии равновероятности, нужна 5 разрядная кодовая комбинация. При учете ВСЕХ статистических связей реальная энтропия составляет около 1,5 бит на букву. Нетрудно показать, что избыточность в данном случае составит

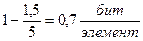, (1.25)

Если средняя загрузка единичного элемента так мала, встает вопрос, нельзя ли уменьшить среднее количество элементов необходимых для переноса одного сообщения и как наиболее эффективно это сделать?

Для решения этой задачи используются неравномерные коды.

При этом, для передачи сообщения, содержащего большее количество информации, выбирают более длинную кодовую комбинацию, а для передачи сообщения с малым объемом информации используют короткие кодовые комбинации.

Учитывая, что объем информации, содержащейся в сообщении, определяется вероятностью появления

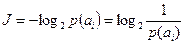, (1.26)

можно перефразировать данное высказывание.

Для сообщения, имеющего высокую вероятность появления, выбирается более короткая комбинация и наоборот, редко встречающееся сообщение кодируется длинной комбинацией.

Т.о. на одно сообщение будет затрачено в среднем меньшее единичных элементов 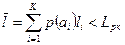, чем при равномерном.

Если скорость телеграфирования постоянна, то на передачу одного сообщения будет затрачено в среднем меньше времени

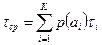(1.27)

А значит, при той же скорости телеграфирования будет передаваться большее число сообщений в единицу времени, чем при равномерном кодировании, т.е. обеспечивается большая скорость передачи информации.

Каково же в среднем минимальное количество единичных элементов требуется для передачи сообщений данного источника?

Ответ на этот вопрос дал Шеннон.

Шеннон показал, что

1. Нельзя закодировать сообщение двоичным кодом так, что бы средняя длина кодового слова 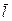была численно меньше величины энтропии источника сообщений

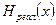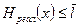. , (1.28)

где .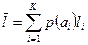

2. Существует способ кодирования, при котором средняя длина кодового слова немногим отличается от энтропии источника

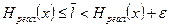(1.29)

Остается выбрать подходящий способ кодирования.

Эффективность применения оптимальных неравномерных кодов может быть оценена:

1. Коэффициентом статистического сжатия, который характеризует уменьшение числа двоичных элементов на сообщение, при применении методов эффективного кодирования в сравнении с равномерным 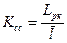. Учитывая, что 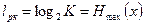, можно записать 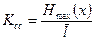. К_сс лежит в пределах от 1 - при равномерном коде до 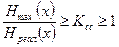, при наилучшем способе кодирования.

2. Коэффициент относительной эффективности

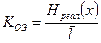- позволяет сравнить эффективность применения различных методов эффективного кодирования.

В неравномерных кодах возникает проблема разделения кодовых комбинаций. Решение данной проблемы обеспечивается применением префиксных кодов.

Префиксным называют код, для которого никакое более короткое слово не является началом другого более длинного слова кода. Префиксные коды всегда однозначно декодируемы.

Введем понятие кодового дерева для множества кодовых слов.

Наглядное графическое изображение множества кодовых слов можно получить, установив соответствие между сообщениями и концевыми узлами двоичного дерева. Пример двоичного кодового дерева изображен на рисунке. 1.

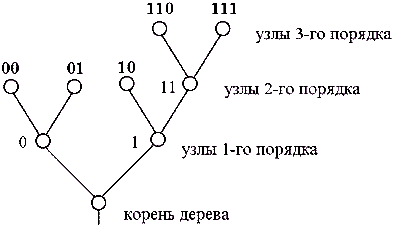
Рисунок 1.16. Пример двоичного кодового дерева

Две ветви, идущие от корня дерева к узлам первого порядка, соответствуют выбору между “0” и “1” в качестве первого символа кодового слова: левая ветвь соответствует “0”, а правая – “1”. Две ветви, идущие из узлов первого порядка, соответствуют второму символу кодовых слов, левая означает “0”, а правая – “1” и т. д. Ясно, что последовательность символов каждого кодового слова определяет необходимые правила продвижения от корня дерева до концевого узла, соответствующего рассматриваемому сообщению.

Формально кодовые слова могут быть приписаны также промежуточным узлам. Например, промежуточному узлу второго порядка на рисунок .1 можно приписать кодовое слово 11, которое соответствует первым двум символам кодовых слов, соответствующих концевым узлам, порождаемых этим узлом. Однако кодовые слова, соответствующие промежуточным узлам, не могут быть использованы для представления сообщений, так как в этом случае нарушается требование префиксности кода.

Требование, чтобы только концевые узлы сопоставлялись сообщениям, эквивалентно условию, чтобы ни одно из кодовых слов не совпало с началом (префиксом) более длинного кодового слова.

Любой код, кодовые слова которого соответствуют различным концевым вершинам некоторого двоичного кодового дерева, является префиксным, т. е. однозначно декодируемым.

Метод Хаффмена

Одним из часто используемых методов эффективного кодирования является так называемый код Хаффмена.

Пусть сообщения входного алфавита 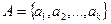имеют соответственно вероятности их появления .

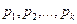Тогда алгоритм кодирования Хаффмена состоит в следующем:

1. Сообщения располагаются в столбец в порядке убывания вероятности их появления.

2. Два самых маловероятных сообщения объединяем в одно сообщение b, которое имеет вероятность, равную сумме вероятностей сообщений 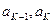, т. е. 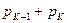. В результате получим сообщения 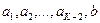, вероятности которых .

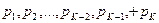3. Повторяем шаги 1 и 2 до тех пор, пока не получим единственное сообщение, вероятность которого равна 1.

4. Проводя линии, объединяющие сообщения и образующие последовательные подмножества, получаем дерево, в котором отдельные сообщения являются концевыми узлами. Соответствующие им кодовые слова можно определить, приписывая правым ветвям объединения символ “1”, а левым - “0”. Впрочем, понятия “правые” и “левые” ветви в данном случае относительны.

Рисунок 1.17 – Алгоритм расчета точек ветвей дерева Хаффмена

На основании полученной таблицы можно построить кодовое дерево

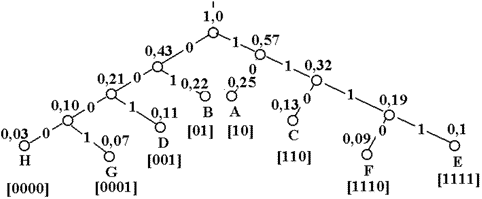
Рисунок 1.18 – Дерево Хаффмена

Так как в процессе кодирования сообщениям сопоставляются только концевые узлы, полученный код является префиксным и всегда однозначно декодируем.

При равномерных кодах одиночная ошибка в кодовой комбинации приводит к неправильному декодированию только этой комбинации. Одним из серьёзных недостатков префиксных кодов является появление трека ошибок, т.е. одиночная ошибка в кодовой комбинации, при определенных обстоятельствах, способна привести к неправильному декодированию не только данной, но и нескольких последующих кодовых комбинаций.

Пример на однозначность декодирования и трек ошибок

Пусть передавалась следующая последовательность

1 0 0 1 1 1 0 0 0 1

a b c d

При возникновении ошибки в первом двоичном элементе, получим

0 0 0 1 1 1 0 0 0 1

g c d

Т.О. ошибка в одном разряде комбинации первого символа привела к неправильному декодированию двух символов. (Трек ошибок).

От СПДС обычно требуется не только передавать сообщения с заданной скоростью передачи информации, но и обеспечивать при этом требуемую достоверность.

Получив сообщение, пользователь должен быть с высокой степенью уверен, что отправлялось именно это сообщение.

Помехи, действующие в канале, как известно, приводят к возникновению ошибок. Исходная вероятность ошибки в каналах связи обычно не позволяет достичь высокой степени достоверности без применения дополнительных мероприятий. К таким мероприятиям, обеспечивающим защиту от ошибок, относят применения корректирующих кодов.

В общей структурной схеме СПДС задачу защиты от ошибок выполняет кодер и декодер канала, который иногда называют УЗО.