Интерполяционный полином Лагранжа.
Лагранж предложил следующую форму интерполяционного полинома:
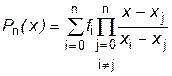
| (5.5) |
Старшая степень аргумента x в этом полиноме равна n, так как каждое произведение в (5.5) содержит n сомножителей типа ( x - x j ).
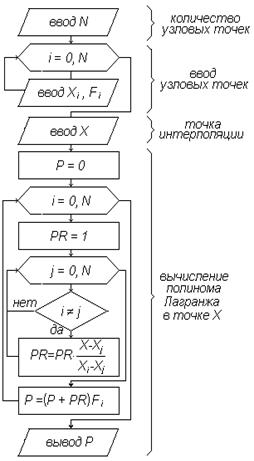 Рис.5.3. Алгоритм интерполяции
с использованием полинома
Лагранжа
Рис.5.3. Алгоритм интерполяции
с использованием полинома
Лагранжа
| В узлах x = x i выполняются условия Лагранжа Pn (x i )=f i. Например, при n=3 полином Лагранжа выглядит следующим образом:
P3(x)=f0 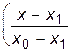 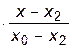 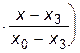 +
+ f1 +
+ f1 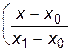 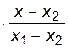 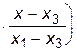 +
+ f2 +
+ f2 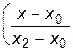 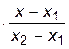 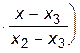 +
+ f3 +
+ f3 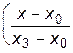 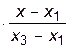 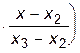 .
Тогда, например, при x = x2 получаем:
P3(x2)=f0 .
Тогда, например, при x = x2 получаем:
P3(x2)=f0 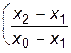 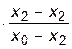 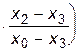 +
+ f1 +
+ f1 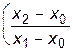 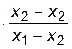 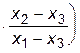 +
+ f2 +
+ f2 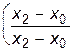 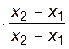 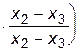 +
+ f3 +
+ f3 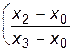 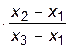 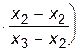 . .
|
Сомножители при f0, f1 и f3 из-за наличия члена x2 - x2 обращаются в ноль, а сомножитель при f2 равен единице, т.е. P3(x2)=f2, что и требовалось доказать.
Блок-схема интерполяции полиномом Лагранжа приведена на рис.5.3.
В отличие от канонического полинома для вычислений значений полинома Лагранжа не требуется предварительного определения коэффициентов полинома, но для каждой новой точки интерполяции полином приходится пересчитывать вновь. Поэтому практическое применение полинома Лагранжа оправдано в том случае, когда интерполяция проводится в сравнительно небольшом количестве точек.
Дата добавления: 2015-01-15; просмотров: 3670;
