Силы и моменты инерции. Частные случаи их определения

Пусть тело движется под действием приложенных к нему сил 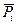и моментов 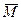_і.Их равнодействующие сила и момент равны:

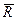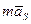= и = ,

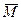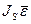где m – масса тела, кг;

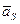– ускорение центра масс тела, м/с²;

J_S – момент инерции тела относительно оси, проходящей через центр масс, кг·м²;

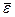– угловое ускорение тела, с^-2.

Если к телу приложить силу и момент инерции, которые равны

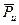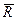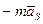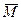= – = , _и = – = – ,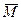

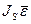то по принципу Д'Аламбера устанавливается квазистатическое равновесие и расчет можно производить по уравнениям статики.

		Рис. 7.1. Сила и момент инерции в общем случае		Рис. 7.2. Сила и момент инерции в поступательном движении

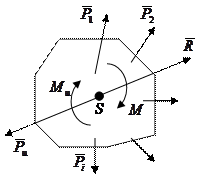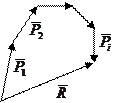Рассмотрим частные случаи определения сил и моментов инерции для разных видов движения звеньев.

1. Тело совершает поступательное движение (рис. 7.2). Момент инерции равен нулю, так как угловое ускорение равно нулю. Сила инерции приложена в центре масс и противоположна его ускорению.

2. Тело совершает вращательное движение вокруг оси, проходящей через центр масс (рис. 7.3, а). В этом случае сила инерции равна нулю, так как центр масс не подвижен. На тело действует только момент инерции, противоположный угловому ускорению.

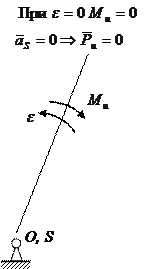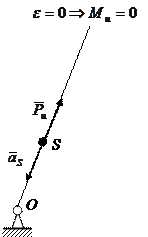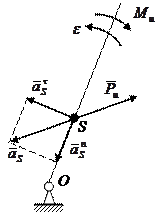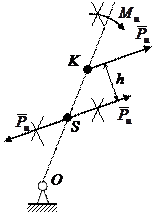а) б) в) г)

3. Тело совершает вращательное движение вокруг оси, не проходящей через центр масс (рис. 7.3, б). На тело действует момент инерции, противоположный угловому ускорению, и сила инерции, приложенная в центре масс и противоположна его ускорению.

Если угловая скорость постоянна, то сила инерции параллельна звену и направлена от центра вращения (рис. 7.3, в).

Для выполнения расчетов удобно заменять силу и момент инерции одной равнодействующей силой инерции (рис. 7.3, г). Для этого момент инерции представляют как пару сил, равных по величине силе инерции, с плечом h: 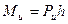. Одна из этих сил приложена в центре масс противоположно силе инерции, а вторая в некоторой точке К звена так, чтобы сохранялось направление момента инерции (т.е. точка К лежит дальше от центра вращения, чем центр масс).

Силы в центре масс взаимно уравновешиваются. В результате вместо системы с моментом инерции и силой инерции, приложенной в центре масс, получаем одну силу инерции, приложенную в точке К, которую называют точкой качания звена. Расстояние от центра масс до точки К определяется по формуле:

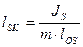, м.

4. Шатун АВ находится в сложном движении. На тело действует момент инерции, противоположный угловому ускорению, и сила инерции, приложенная в центре масс и противоположна его ускорению.

Для замены силы инерции и момента инерции одной равнодействующей силой инерции (рис. 7.4) рассматриваем движение шатуна как поступательное движение вместе с точкой А и вращательное движение вокруг точки А. Тогда равнодействующая сила инерции складывается из двух сил инерции: силы инерции в поступательном движении 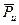^/ и силы инерции во вращательном движении 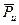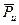^//: ^/= - m 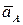, 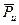^//= - m 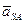. Сила 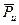^/проходит через центр масс S и направлена противоположно ускорению 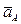. Сила инерции 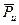^//проходит через центр качания шатуна точку К и направлена противоположно ускорению 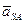(здесь сила 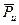^// является равнодействующей силы инерции и момента инерции в относительном вращательном движении (см. п.3)).

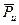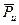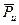Равнодействующая сил инерции , являясь суммой сил ^/ и ^//, проходит через точку пересечения Т (полюс инерции) линий действий этих сил, направлена противоположно ускорению центра тяжести 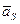. Условная точка Т^/ приложения силы 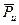будет находиться на пересечении ее линии действия с шатуном.

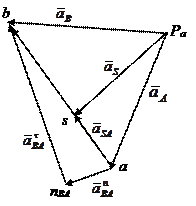Рис. 7.4. Сила и момент инерции в сложном движении