Пример 1.
Структурная группа 2-го класса, 1-го вида (рис. 7.5, а,б)
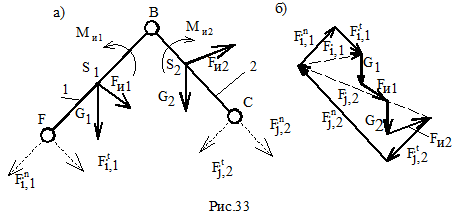 Fi,1t определяется из уравнения моментов для звена 1 - ∑МB=0 относительно т. В. (рис.7.5, а);
Fi,1t определяется из уравнения моментов для звена 1 - ∑МB=0 относительно т. В. (рис.7.5, а);
Fj,2t определяется из уравнения моментов для звена 2 - ∑МВ=0 относительно т. В (рис.7.5,а).
|
Fi,1n и Fj,2n определяются из плана сил (рис.7.5,б), полученного на основе векторного уравнения;
∑Fk=0, где Fk – силы, действующие на структурную группу.
Структурная группа 2-го класса, 2-го вида (рис.7.6, а, б)
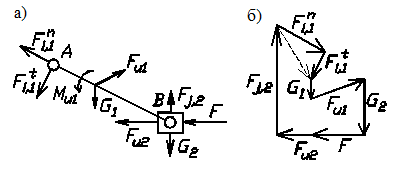 Fj,2 определяется из уравнения моментов - ∑МА=0 относительно т. А. Fi,1=Fi,1n+Fi,1t определяется из плана сил (рис.7.6,б) на основе векторного уравнения ∑Fk=0.
Fj,2 определяется из уравнения моментов - ∑МА=0 относительно т. А. Fi,1=Fi,1n+Fi,1t определяется из плана сил (рис.7.6,б) на основе векторного уравнения ∑Fk=0.
|
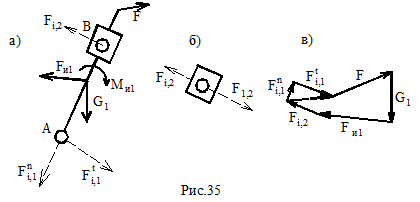 Структурная группа 2-го класса, 3-го вида (рис.7.7, а)
Структурная группа 2-го класса, 3-го вида (рис.7.7, а)
Fj,2 определяется из уравнения моментов - ∑МА=0.
|
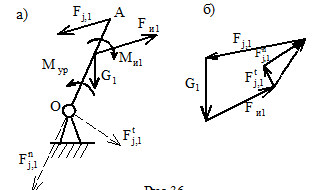 Входное (начальное) звено (рис.7.8, а).
Входное (начальное) звено (рис.7.8, а).
Мур определяется из уравнения моментов - ∑Мо=0.
Fj,1=Fj,1n+Fj,1t определяется из плана сил (рис.7.8,б) согласно векторному уравнению ∑Fk=0.
|
7. Определение уравновешивающей силы (момента) по теореме о «жёстком рычаге» Жуковского
Теорема о «жестком рычаге» Жуковского используется для определения уравновешивающей силы 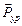 или уравновешивающего момента
или уравновешивающего момента 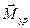 без предварительного определения реакций в кинематических парах механизма и является графической интерпретацией принципа возможных перемещений точек приложения сил. Для реального механизма эти возможные перемещения являются реальными.
без предварительного определения реакций в кинематических парах механизма и является графической интерпретацией принципа возможных перемещений точек приложения сил. Для реального механизма эти возможные перемещения являются реальными.
Исходя из принципа сохранения энергии сумма работ всех внешних сил, приложенных к звеньям механизма, равна нулю. Это условие можно записать в виде
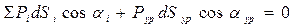 , (3.7)
, (3.7)
где Pi – все внешние силы, в том числе силы полезного и вредного сопротивления, силы инерции и веса, действующие на звенья механизма (силы реакции здесь не учитываются);
dSi – элементарные перемещения точек приложения этих сил;
ai – угол приложения внешних сил, или угол давления (угол между вектором силы и вектором скорости).
Разделим уравнение (3.7) на бесконечно малый интервал времени dt и получим (при условии, что dS/dt = 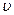 )
)
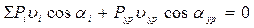 , (3.8)
, (3.8)
то есть сумму мгновенных мощностей, равную нулю.
Для определения величины мгновенных мощностей можно выполнить решение в следующей графической интерпретации.
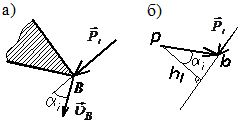 Дано звено с известной скоростью
Дано звено с известной скоростью 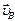 точки В и приложенной к этой точке силой
точки В и приложенной к этой точке силой 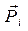 (рис. 3.13). Построим план скоростей, повёрнутый на 900, где
(рис. 3.13). Построим план скоростей, повёрнутый на 900, где 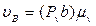 ,
, 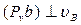 . Вычислим момент силы
. Вычислим момент силы 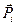 относительно полюса Рv плана скоростей:
относительно полюса Рv плана скоростей:
|
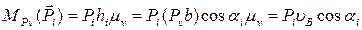 .
.
С учётом этого уравнение (3.8) можно записать как 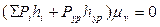 .
.
Так как масштаб 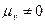 , то можно сформулировать теорему Жуковского:
, то можно сформулировать теорему Жуковского:
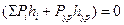 (3.9)
(3.9)
или алгебраическая сумма моментов всех внешних сил (включая силы инерции), перенесенных с механизма в соответствующие точки повёрнутого на 900 плана скоростей, относительно полюса равна нулю.
Последовательность определения Pур в механизме по теореме Жуковского:
1. Построить повёрнутый на 900 (в любую сторону) план скоростей механизма.
2. В соответствующие точки плана скоростей нанести все ранее определённые внешние силы (включая силы инерции и силы веса), действующие на механизм, в том числе и уравновешивающую силу Pур.
3. Составить уравнение вида (3.9). Плечи моментов сил брать из повёрнутого плана скоростей.
4. Из составленного уравнения определить Pур.
Пример 2.Заданы внешние силы, действующие на звенья механизма Р2 и Р3. Найдём уравновешивающую силу Рур, для чего построим план механизма в масштабе длин (рис. 3.14) и повёрнутый на 900 план скоростей (рис. 3.15).
Приложим силы в соответствующие точки k и b3 повёрнутого плана скоростей, обозначаем плечи сил. Составляем уравнение моментов сил относительно полюса плана скоростей:

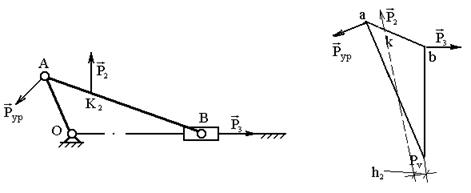
Рис. 3.14. План механизма Рис. 3.15. Повёрнутый на 900
план скоростей
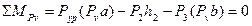 . Отсюда
. Отсюда 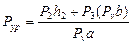 .
.
Если сила Pур получается с отрицательным знаком, то её предварительно выбранное направление следует поменять на противоположное.
8. Силовой анализ рычажных механизмов с учетом сил трения
Трение в поступательной кинематической паре
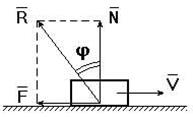
При перемещении одного тела (звена механизма) относительно находящегося с ним в контакте другого тела (звена) в месте их контакта возникает сила, сопротивляющаяся перемещению, – сила трения F (рис. 3.16).
Величину коэффициента трения в поступательной кинематической паре можно определить с помощью так называемого закона Кулона, в соответствии с которым величина силы трения F прямо пропорциональна нормальной силе N между соприкасающимися звеньями. Векторная сумма сил 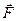 и
и 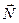 равна полной силе реакций в кинематической паре:
равна полной силе реакций в кинематической паре: 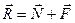 (рис. 3.16).
(рис. 3.16).
Отношение 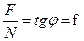 называют коэффициентом трения скольжения в поступательной кинематической паре, а угол
называют коэффициентом трения скольжения в поступательной кинематической паре, а угол 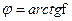 – углом трения скольжения.
– углом трения скольжения.
Полная реакция 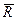 отклоняется на угол трения
отклоняется на угол трения 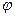 в сторону, противоположную скорости
в сторону, противоположную скорости 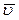 (см. рис. 3.16).
(см. рис. 3.16).
Величину коэффициента трения скольжения f можно определить экспериментально или по справочникам (величина f зависит от шероховатости, материалов, трущихся поверхностей, наличия смазки, ее качества, температуры и т.д.).
| 
|
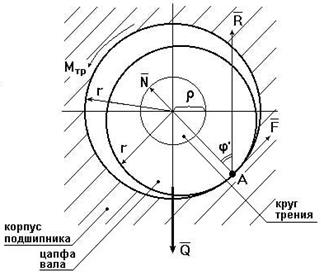
| Рис. 3.16. Схема сил в поступательной кинематической паре | Рис. 3.17. Схема сил во вращательной кинематической паре |
Трение во вращательной кинематической паре
Внешние нагрузки, действующие на вал при его вращении, показаны на схеме рис. 3.17. Здесь А – точка приложения нормальной реакции 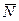 , причем
, причем 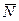 – равно-действующая всех нор-мальных сил (эпюра этих сил может иметь различный вид), (рис. 3.18);
– равно-действующая всех нор-мальных сил (эпюра этих сил может иметь различный вид), (рис. 3.18); 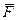 – сила трения (равно-действующая всех сил трения, распределенных по поверхности контакта);
– сила трения (равно-действующая всех сил трения, распределенных по поверхности контакта); 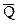 – сила давления цапфы вала на опору (корпус подшипника);
– сила давления цапфы вала на опору (корпус подшипника); 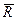 – сила реакции во вращательной кинематической паре,
– сила реакции во вращательной кинематической паре, 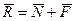 ;
; 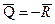 ;
; 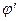 – угол трения; r – радиус цапфы (опорной части) вала;
– угол трения; r – радиус цапфы (опорной части) вала; 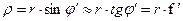 – радиус круга трения;
– радиус круга трения; 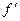 – приведенный коэффициент трения.
– приведенный коэффициент трения.
Во вращательной кинематической паре (см. рис. 3.15) реакция 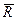 отстоит от оси вращения на величину радиуса круга трения
отстоит от оси вращения на величину радиуса круга трения 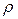 , причем
, причем 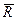 всегда касательна к кругу трения.
всегда касательна к кругу трения.
Момент трения 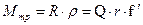 .
.
Величину 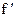 можно определить экспериментально или по эмпирическим формулам с учетом износа подшипника и соответствующего изменения эпюр давления (рис. 3.18): для нового подшипника
можно определить экспериментально или по эмпирическим формулам с учетом износа подшипника и соответствующего изменения эпюр давления (рис. 3.18): для нового подшипника 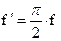 , для изношенного –
, для изношенного – 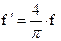 , где f – коэффициент трения скольжения в поступательной кинематической паре (берется из справочников).
, где f – коэффициент трения скольжения в поступательной кинематической паре (берется из справочников).
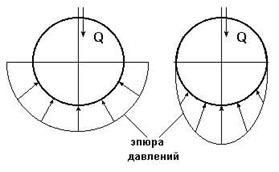
Рис. 3.18. Примерные схемы эпюр давления в новом и изношенном подшипниках скольжения
Трение качения в высшей кинематической паре
Картину внешних сил и эпюр распределения давлений в месте контакта тел качения можно условно отобразить на нижеприведенных схемах (рис. 3.19). В состоянии покоя эпюра напряжений в зоне контакта симметрична относительно общей нормали, проведенной через условную точку касания, а равнодействующая сила N совпадает с нормалью. При качении симметрия эпюры нарушается, а сила N смещается в направлении качения на расстояние k.
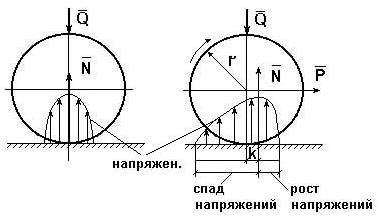
а б
Рис. 3.19. Примерные схемы сил и эпюр давления
в зоне контакта цилиндра с плоскостью: а – состояние покоя;
б – состояние перекатывания
Здесь  – равнодействующая сила давлений в месте смятия соприкасающихся звеньев (тел качения);
– равнодействующая сила давлений в месте смятия соприкасающихся звеньев (тел качения); 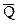 – нагружающая сила,
– нагружающая сила, 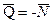 ;
; 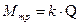 – момент трения качения;
– момент трения качения; 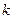 – плечо силы трения качения или коэффициент трения качения (имеет размерность длины);
– плечо силы трения качения или коэффициент трения качения (имеет размерность длины); 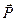 – сила перекатывания.
– сила перекатывания.
Условие равновесия перекатывающегося тела в форме моментов можно записать как 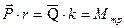 , откуда
, откуда 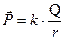 .
.
Дата добавления: 2015-01-19; просмотров: 1440;
