Построение аппроксимирующих моделей
Для подбора коэффициентов моделей используют регрессионный анализ. Пусть имеются наблюдения прогнозируемого показателя 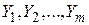 , заданные значениями
, заданные значениями  , связанные условием:
, связанные условием:
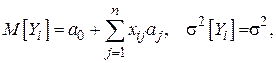
где 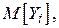
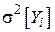 - математическое ожидание и дисперсия случайной величины
- математическое ожидание и дисперсия случайной величины 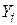 ;
;
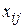 - известные значения параметров;
- известные значения параметров;
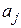 - неизвестные коэффициенты.
- неизвестные коэффициенты.
Для случая прогнозирования временных зависимостей 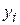 - наблюдения прогнозируемого показателя, соответствующие моментам времени
- наблюдения прогнозируемого показателя, соответствующие моментам времени 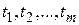 .
.
Регрессионный анализ позволяет наилучшим образом подобрать коэффициенты 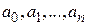 на основе имеющейся выборки
на основе имеющейся выборки  .
.
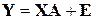 ,
,
где 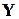 - вектор наблюдений
- вектор наблюдений  ;
;
 - вектор искомых коэффициентов
- вектор искомых коэффициентов 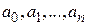 ;
;
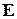 - вектор отклонений наблюдений от своих математических ожиданий
- вектор отклонений наблюдений от своих математических ожиданий 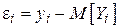 ;
;
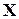 - план-матрица, состоящая из
- план-матрица, состоящая из 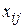 . Она содержит
. Она содержит 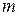 строк по числу наблюдений и
строк по числу наблюдений и 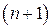 столбец по числу факторов.
столбец по числу факторов.
Оптимальным значениям 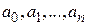 соответствует минимум функции
соответствует минимум функции
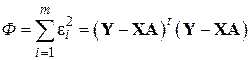 .
.
Это выражение называют критерием наименьших квадратов. Дифференцируя по 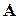 и приравнивая к нулю
и приравнивая к нулю  , получим
, получим
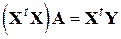 ,
,
откуда найдём  .
.
Линейные уравнения, позволяющие найти искомые значения компонент вектора  , называются система нормальных уравнений.
, называются система нормальных уравнений.
В простейшем случае  .
.
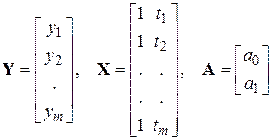 .
.
Система нормальных уравнений имеет следующий вид
 .
.
Выполнив умножения матриц, получим
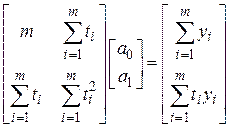 .
.
Определитель системы двух линейных уравнений равен
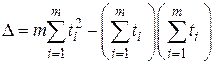 .
.
Искомые коэффициенты равны

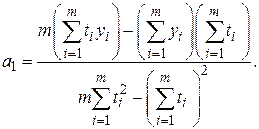
Для оценки точности вычисляют кажущуюся погрешность моделирования 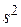
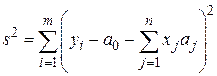 .
.
Важнейшие требования к план-матрице 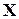 - линейная независимость её столбцов и хорошая обусловленность матрицы
- линейная независимость её столбцов и хорошая обусловленность матрицы 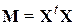 .
.
Проверка статистической состоятельности построенной регрессионной модели.
Наиболее простой критерий – «нулевая гипотеза». Она опровергает гипотезу, положенную в основу моделирования, т.е. предполагает, что построенная модель не улавливает закономерности изменения случайных величин. Для проверки вычисляют
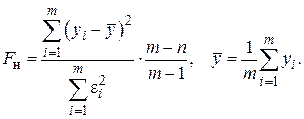
Найденное число представляет собой значение случайной величины, которая при справедливости «нулевой гипотезы» распределены по закону 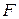 -распределения с
-распределения с  степенью свободы числителя и
степенью свободы числителя и 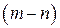 степенями свободы знаменателя. Задаваясь вероятностью
степенями свободы знаменателя. Задаваясь вероятностью 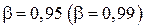 , можно по таблицам найти верхнюю границу
, можно по таблицам найти верхнюю границу 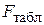 . Если
. Если 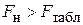 , то «нулевая гипотеза» не верна и модель выбрана правильно.
, то «нулевая гипотеза» не верна и модель выбрана правильно.
Согласование моделей прогнозирования.
Приведённые модели прогнозирования не учитывают взаимосвязи между крупными узлами ОЭС и ОЭС в целом. Рассмотрим простейший метод прогнозирования временных зависимостей, учитывающий эти связи.
Пусть имеется 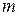 наблюдений
наблюдений 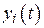 для узлов
для узлов  , входящих в ОЭС (
, входящих в ОЭС ( 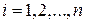 ) и наблюдение
) и наблюдение 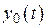 того же показателя для ОЭС в целом. Согласовать прогнозы так, чтобы:
того же показателя для ОЭС в целом. Согласовать прогнозы так, чтобы:
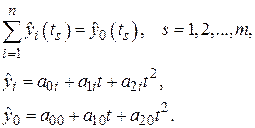
Чтобы обеспечить согласованность прогнозов узлов и ОЭС необходимо добавить следующую систему ограничений:
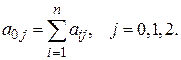
С учётом этого ограничения
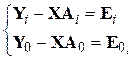
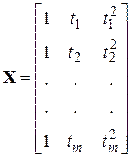 ,
,
где 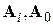 - векторы искомых коэффициентов
- векторы искомых коэффициентов 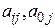 .
.
Используя метод наименьших квадратов, получим
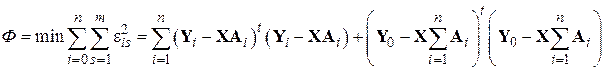 .
.
Дифференцируя, получим
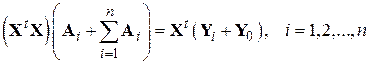 .
.
Откуда можно найти 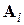 .
.
Дата добавления: 2015-01-15; просмотров: 1383;
