Логистическое уравнение

Рассмотрим простое уравнение, применяемое для исследования роста численности популяции бактерий, животных и даже людей. Первую модель динамики роста населения Земли создал Мальтус. Он предположил, что скорость изменения численности населения 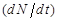определяется самой численностью населения 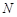в этот момент времени и коэффициентами рождаемости 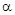и смертности :

.

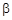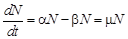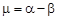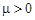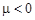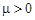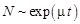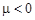Здесь . Если рождаемость превышает смертность, то . Если смертность больше, чем рождаемость, . Это уравнение легко решается. При численность населения неограниченно возрастает по экспоненциальному закону . При численность населения убывает и стремится к нулю по тому же закону 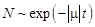. Исходя из этой модели Мальтус сделал вывод о скором перенаселении Земли.

В то же время давно было замечено, что в популяциях животных экологическая система стабилизируется, т. е. численность животных через некоторое время перестает изменяться. Это обстоятельство толкнуло Ферхюльста в 1838 г. усовершенствовать модель Мальтуса и предложить логистическую модель:

.

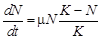Здесь 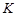– емкость среды или предельная численность, которой может достичь популяция. Решением этого уравнения будет функция

,

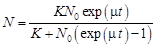где 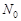– численность популяции в начальный момент времени .

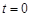Это решение при малых временах ведет себя так же, как решение Мальтуса, но на больших временах 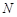стремится к 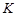. Таким образом, возникает устойчивое состояние популяции при 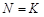. Это состояние может изменяться под действием климатических условий или конкуренции других популяций за кормовую базу. При этом в уравнении будут изменяться коэффициенты 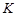и 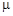. Если имеется две популяции, которые конкурируют за емкость среды, то необходимо решать два логистических уравнения, коэффициенты 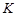в которых связаны друг с другом (например, 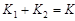). В этом случае логистические уравнения позволяют рассчитать условия сосуществования двух популяций или гибели одной из них.

Логистические уравнения имеют достаточно простой вид, но приводят к большому разнообразию решений. Они описывают разнообразные явления не только в экологии. При помощи этих уравнений моделируются рост колонии дрожжевых грибов, динамика основных видов энергетических ресурсов, динамика распространения компьютеров на японском рынке, динамика построения метрополитена в разных городах мира и даже число людей, убитых «Красными бригадами» в Италии.

В заключение отметим, что логистическое уравнение является наиболее простым и активно используется в синергетике. Существует множество моделей, гораздо более сложных, которые предсказывают нетривиальное поведение открытых систем вдали от термодинамического равновесия.

Литература

Кудрявцев П.С. Курс истории физики. – М.: Просвещение, 1982. – 447 с.

Нараянамурти В. Кристаллические полупроводниковые гетероструктуры // Физика за рубежом. – М.: Мир, 1986. – С. 100–121.

Пригожин И., Кондепуди Д. Современная термодинамика. – М.: Мир, 2002. – 461 с.

Кикоин А.К., Кикоин И.К. Молекулярная физика. – М.: Наука, 1976. – 480 с.