Статистическая интерпретация энтропии
Энтропия, введенная нами ранее, определяется как термодинамическая величина, т. е. параметр, характеризующий систему в целом.
С точки зрения молекулярно-кинетической теории как обратимые, так и необратимые процессы обусловлены движением молекул. Движение самих молекул подчиняется законам механики, которые обратимы во времени, поэтому на механическом уровне описания не существует преимущественного движения молекул, при котором энтропия должна возрастать. Например, если в некотором сосуде создать такое распределение молекул газа, что в одной его половине будет больше молекул, чем в другой, то согласно законам механики газ может перетекать как из первой половины во вторую, так и, наоборот, из половины с меньшим содержанием молекул в половину с большим их содержанием.
В то же время с точки зрения термодинамики последний процесс невозможен, так как понижает энтропию системы.
Чтобы объяснить это противоречие, австрийский физик Л. Больцман ввел в науку понятие термодинамической вероятности 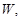 которую иногда называют также статистическим весом. Эта величина соответствует числу микросостояний системы, отвечающей одному и тому же макросостоянию. Макросостояние термодинамической системы характеризуется распределением термодинамических параметров (температуры, давления, энергии и т. д.) по объему, занимаемому системой. Микросостояние – это совокупность координат и скоростей всех молекул системы. Оказывается, одному макросостоянию соответствует множество микросостояний, т. е. немного разные скорости и координаты молекул в системе создают одни и те же термодинамические параметры, характеризующие систему. Число микросостояний
которую иногда называют также статистическим весом. Эта величина соответствует числу микросостояний системы, отвечающей одному и тому же макросостоянию. Макросостояние термодинамической системы характеризуется распределением термодинамических параметров (температуры, давления, энергии и т. д.) по объему, занимаемому системой. Микросостояние – это совокупность координат и скоростей всех молекул системы. Оказывается, одному макросостоянию соответствует множество микросостояний, т. е. немного разные скорости и координаты молекул в системе создают одни и те же термодинамические параметры, характеризующие систему. Число микросостояний 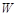 будет различным для разных макросостояний, причем, чем больше макросостояние отличается от равновесного, тем меньшее
будет различным для разных макросостояний, причем, чем больше макросостояние отличается от равновесного, тем меньшее 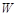 ему соответствует. Максимальной термодинамической вероятностью
ему соответствует. Максимальной термодинамической вероятностью 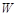 обладает равновесное состояние системы. Согласно Л. Больцману, эволюция системы представляет собой постоянную смену микросостояний, причем каждое следующее микросостояние возникает в системе случайно, хотя через достаточно малый промежуток времени слабо отличается от предыдущего. Таким образом, механическое движение молекул заменяется статистическим процессом смены микросостояний. Система стремится перейти в такое макросостояние, которое характеризуется наибольшей термодинамической вероятностью
обладает равновесное состояние системы. Согласно Л. Больцману, эволюция системы представляет собой постоянную смену микросостояний, причем каждое следующее микросостояние возникает в системе случайно, хотя через достаточно малый промежуток времени слабо отличается от предыдущего. Таким образом, механическое движение молекул заменяется статистическим процессом смены микросостояний. Система стремится перейти в такое макросостояние, которое характеризуется наибольшей термодинамической вероятностью 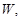 т. е. в равновесное состояние. Хотя система может случайно отклоняться от своего равновесного состояния, эти отклонения очень малы и называются флуктуациями. Следовательно, второе начало термодинамики можно сформулировать на языке Л. Больцмана: система стремится к максимуму своей термодинамической вероятности W. Л. Больцман связал термодинамическую вероятность с энтропией
т. е. в равновесное состояние. Хотя система может случайно отклоняться от своего равновесного состояния, эти отклонения очень малы и называются флуктуациями. Следовательно, второе начало термодинамики можно сформулировать на языке Л. Больцмана: система стремится к максимуму своей термодинамической вероятности W. Л. Больцман связал термодинамическую вероятность с энтропией 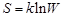 , где k – постоянная Больцмана.
, где k – постоянная Больцмана.
Поясним это определение на следующем примере. Пусть имеется «газ из четырех молекул». Рассмотрим два макросостояния этого «газа».
Состояние 1: «газ» равномерно занимает весь предоставленный ему объем.
| * * | * * |
Состояние 2: по неизвестной причине «газ» занимает лишь половину предоставленного ему объема – или левую или правую мысленно выделенные половины объема.
| * * * * |
| * * * * |
Согласно классическим представлениям все молекулы в принципе можно различить, пронумеровать и проследить за их поведением.
Легко подсчитать статистический вес W указанных макросостояний. Для первого макросостояния имеется всего шесть способов распределения молекул по двум мысленно выделенным половинам объема. (При этом мы не учитываем возможные различные распределения молекул по скоростям движения – см. ниже).
| № молекул слева | 1, 2 | 1, 3 | 1, 4 | 2, 3 | 2, 4 | 3, 4 |
| № молекул справа | 3, 4 | 2, 4 | 2, 3 | 1, 4 | 1, 3 | 1, 2 |
Таким образом, статистический вес макросостояния 1 равен W1 = 6, а энтропия этого состояния равна 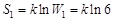 . Для второго макросостояния можно насчитать лишь два способа распределения молекул по мысленно выделенным половинам объема.
. Для второго макросостояния можно насчитать лишь два способа распределения молекул по мысленно выделенным половинам объема.
| № молекул слева | 1, 2, 3, 4 | |
| № молекул справа | 1, 2, 3, 4 |
Таким образом, статистический вес макросостояния 2 равен W2 = 2, а энтропия этого состояния равна 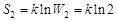 , т. е. энтропия
, т. е. энтропия 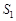 больше энтропии
больше энтропии  .
.
Пусть имеется реальная перегородка, разделяющая объем на две части, и газ первоначально занимает левую половину объема. Если убрать в какой-то момент перегородки, газ самопроизвольно займет весь объем – этот процесс нам почти очевиден. Но дождемся ли мы обратного процесса: вдруг через какой-то промежуток времени газ самопроизвольно снова соберется в левой половине?
Вероятность этого процесса крайне мала. И это утверждение тем вернее, чем больше частиц в газе: для «газа из двух молекул» сравнительно легко представить, что случайно обе молекулы в некоторый момент оказались в одной половине объема («флуктуация»), а вот для реального газа из 100 000 000 000 000 000 000 000 молекул представить подобное практически невозможно. Вероятность такой флуктуации практически равна нулю.
Опыт действительно показывает, что самопроизвольно газ не собирается в какой-либо части предоставленного объема. Наиболее вероятным является равномерное распределение газа по всему предоставленному ему объему, т. е. всегда реально осуществляется наиболее вероятное распределение – макросостояние с наибольшей энтропией.
И это не случайно. Это находится в полном соответствии с установленными законами естествознания.
Следует отметить, что термодинамическая вероятность отличается от обычной вероятности, используемой в теории вероятностей, тем, что она больше единицы и, как правило, имеет огромное значение. Однако при определенных условиях она может приближаться к единице. Например, при приближении абсолютной температуры системы к нулю все молекулы занимают строго определенные состояния. В этом случае макросостоянию системы соответствует одно единственное микросостояние: 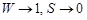 при
при 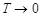 . Это положение носит название третьего начала термодинамики.
. Это положение носит название третьего начала термодинамики.
Мы видим, что энтропия связана с термодинамической вероятностью состояния системы. Саму же термодинамическую вероятность можно понимать как меру упорядоченности состояния системы или, наоборот, меру беспорядка в системе. Чем больше термодинамическая вероятность состояния системы, тем больше в системе беспорядка. Действительно, если молекулы газа находятся в одной половине сосуда, то такая система более упорядочена, чем если бы они были равномерно распределены по всему объему. И вообще, всякое неравновесное состояние является более упорядоченным, чем равновесное. Следовательно, второе начало термодинамики можно переформулировать следующим образом: изолированная система всегда стремится к максимуму беспорядка, а мерой беспорядка является энтропия.
Открытие второго начала термодинамики привело некоторых ученых к идее тепловой смерти Вселенной, т. е. через некоторое достаточно большое время все термодинамические параметры во Вселенной выровняются (погаснут звезды, остынут планеты) и Вселенная превратится в безжизненную груду камней. Это логичный вывод из равновесной термодинамики закрытых систем. Однако многие ученые сомневаются в таком исходе. Их возражения сводятся в основном к двум положениям. Во-первых, даже в равновесии возможны флуктуации термодинамических параметров. В «рамках» огромной Вселенной такие флуктуации могут быть огромными, тем самым постоянно создавая неравновесные состояния в той или иной области пространства. Во-вторых, вряд ли бесконечную Вселенную можно рассматривать как изолированную систему. Скорее, каждую область Вселенной надо рассматривать как открытую систему. Для открытых систем законы равновесной термодинамики не применимы. Более того, открытая система может вообще не иметь состояния равновесия.
Дата добавления: 2015-01-15; просмотров: 1990;
