МОЛЕКУЛЯРНЫЕ МЕХАНИЗМЫ ОПУХОЛЕВОГО РОСТА
В зависимости от природы жидкости и твердого тела работа адгезии складывается из энергий различных взаимодействий (молекулярных, полярных и др.). Молекулярные теории смачивания развиты, в основном, для систем, в которых адгезия обусловлена преимущественно дисперсионными силами. Таковы, например, системы, в которых хотя бы одна из фаз (жидкость или твердое тело) является предельным углеводородом, поскольку связи между молекулами неполярных веществ осуществляются в основном именно дисперсионными силами.
Если взаимодействие между жидкостью и твердым телом носит только дисперсионный характер, межфазное поверхностное натяжение равно:
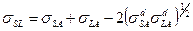 , (1)
, (1)
где 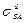 и
и 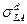 - доли поверхностного натяжения твердого тела и жидкости, которые обусловлены дисперсионными силами.
- доли поверхностного натяжения твердого тела и жидкости, которые обусловлены дисперсионными силами.
Это соотношение было подтверждено измерениями межфазного натяжения на границе несмешивающихся жидкостей.
Из уравнений 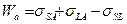 и (1) следует, что работа адгезии
и (1) следует, что работа адгезии 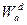 , которая обусловлена дисперсионными силами, равна
, которая обусловлена дисперсионными силами, равна 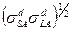 . Это соотношение может быть обосновано с помощью теоретического уравнения для энергии дисперсионного взаимодействия между молекулами веществ 1 и 2:
. Это соотношение может быть обосновано с помощью теоретического уравнения для энергии дисперсионного взаимодействия между молекулами веществ 1 и 2:
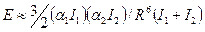 ,
,
Где 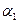 и
и 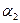 - поляризуемости,
- поляризуемости, 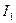 и
и 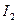 - первые ионизационные потенциалы; R – расстояние между молекулами..
- первые ионизационные потенциалы; R – расстояние между молекулами..
Величина 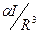 характеризует дисперсионное взаимодействие между молекулами каждой фазы; соответственно она пропорциональна дисперсионной составляющей поверхностного натяжения этой фазы.
характеризует дисперсионное взаимодействие между молекулами каждой фазы; соответственно она пропорциональна дисперсионной составляющей поверхностного натяжения этой фазы.
При смачивании низкоэнергетических твердых тел поверхностное давление, которое создают адсорбированные молекулы жидкости, обычно пренебрежимо мало. Поэтому для расчета краевого угла можно пользоваться уравнениями 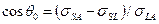 или
или 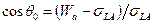 . С учетом соотношения (1) они преобразуются к виду
. С учетом соотношения (1) они преобразуются к виду
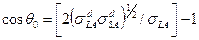 (2)
(2)
Для практического использования этого уравнения нужно знать дисперсионные составляющие поверхностных натяжений твердого тела 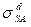 и жидкости
и жидкости 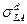 . Для этой цели используют следующий метод. В соответствии с уравнением (2) при смачивании низкоэнергетических твердых тел должна иметь место линейная зависимость
. Для этой цели используют следующий метод. В соответствии с уравнением (2) при смачивании низкоэнергетических твердых тел должна иметь место линейная зависимость 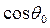 от отношения
от отношения 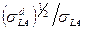 . Прямые, характеризующие смачивание различных подложек, должны проходить через общую точку с координатами (0,-1). Эти выводы хорошо согласуются с экспериментальными данными, например, при контакте различных органических жидкостей с полиэтиленом и парафином. Тангенс угла наклона этих прямых равен
. Прямые, характеризующие смачивание различных подложек, должны проходить через общую точку с координатами (0,-1). Эти выводы хорошо согласуются с экспериментальными данными, например, при контакте различных органических жидкостей с полиэтиленом и парафином. Тангенс угла наклона этих прямых равен 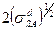 . Отсюда можно рассчитать значения дисперсионной составляющей
. Отсюда можно рассчитать значения дисперсионной составляющей 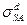 поверхностного натяжения твердых тел. Ниже приведено несколько примеров:
поверхностного натяжения твердых тел. Ниже приведено несколько примеров:
| Твердое тело | Полигекса- фторпропилен | Тефлон | Парафин | Полиэтилен | Полистирол |
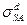 ,мДж/м2 ,мДж/м2
| 18,0 | 19,5 | 21,0 | 35,0 | 44,0 |
Для построения графиков cosθ = f[ 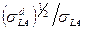 ] вначале измеряют краевые углы при смачивании подложки предельными углеводородами, для которых
] вначале измеряют краевые углы при смачивании подложки предельными углеводородами, для которых 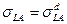 . Поскольку все прямые должны пройти через точку (0, -1), этих измерений достаточно, чтобы провести соответствующую прямую. Отсюда, зная поверхностное натяжение жидкости
. Поскольку все прямые должны пройти через точку (0, -1), этих измерений достаточно, чтобы провести соответствующую прямую. Отсюда, зная поверхностное натяжение жидкости 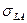 , можно рассчитать и величину
, можно рассчитать и величину 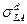 :
:
| Жидкость | Диметил- силоксан | Трикрезил- фосфат | Иодист. метилен | Форма- мид | Гли- церин | Вода | Ртуть |
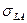 ,
мДж/м2 ,
мДж/м2
| 40,9 | 50,8 | 58.2 | 63,7 | 72,6 | ||
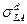 ,
мДж/м2 ,
мДж/м2
| 16,5 | 39,2 | 48,5 | 39,5 | 37,0 | 21,8 |
Сложнее найти дисперсионную составляющую поверхностного натяжения высокоэнергетических твердых тел. В таких системах в общем случае необходимо учитывать влияние поверхностного давления адсорбированных молекул жидкой фазы. Поэтому для оценки 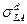 следует предварительно независимыми методами (на основании адсорбционных изотерм) определить поверхностное давление. Другой способ основан на том, что при полном погружении твердого тела в жидкость изменение свободной поверхностной энергии системы (в расчете на единицу площади)
следует предварительно независимыми методами (на основании адсорбционных изотерм) определить поверхностное давление. Другой способ основан на том, что при полном погружении твердого тела в жидкость изменение свободной поверхностной энергии системы (в расчете на единицу площади) 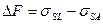 . Воспользовавшись уравнением (1), получим
. Воспользовавшись уравнением (1), получим 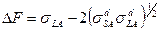 . В свою очередь величину ΔF можно найти независимо из калориметрических измерений теплоты смачивания и температурной зависимости краевого угла.
. В свою очередь величину ΔF можно найти независимо из калориметрических измерений теплоты смачивания и температурной зависимости краевого угла.
Для систем, в которых наряду с дисперсионными силами значительный вклад в работу адгезии вносят молекулярные силы другой природы, для расчета поверхностного натяжения на границе твердое тело – жидкость применяют уравнение
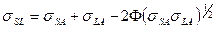 (3)
(3)
Безразмерный коэффициент 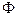 зависит от свойств контактирующих фаз (1 и 2). В наиболее общем виде
зависит от свойств контактирующих фаз (1 и 2). В наиболее общем виде 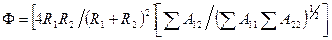 . Здесь
. Здесь 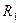 и
и 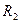 - молекулярные радиусы, соответствующие равновесным расстояниям между молекулами каждой фазы;
- молекулярные радиусы, соответствующие равновесным расстояниям между молекулами каждой фазы; 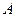 - константа, характеризующая силы притяжения, когда потенциал взаимодействия
- константа, характеризующая силы притяжения, когда потенциал взаимодействия 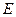 описывается уравнением Леннард – Джонса
описывается уравнением Леннард – Джонса 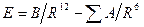 ,
, 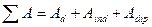 , где
, где 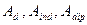 - характеризуют соответственно дисперсионные, индукционные и дипольные взаимодействия;
- характеризуют соответственно дисперсионные, индукционные и дипольные взаимодействия; 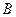 - коэффициент, который характеризует силы отталкивания.
- коэффициент, который характеризует силы отталкивания.
Значения коэффициента 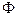 обычно определяют опытным путем – на основании измерений краевых углов при смачивании твердых тел с известным поверхностным натяжением (преимущественно – низкоэнергетических поверхностей), а также с помощью измерений поверхностных натяжений на границе двух жидкостей. В частности, при контакте предельных жидких углеводородов с водой
обычно определяют опытным путем – на основании измерений краевых углов при смачивании твердых тел с известным поверхностным натяжением (преимущественно – низкоэнергетических поверхностей), а также с помощью измерений поверхностных натяжений на границе двух жидкостей. В частности, при контакте предельных жидких углеводородов с водой 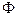 = 0,5 – 0,6. С учетом уравнения (3) равновесный краевой угол определяется уравнением
= 0,5 – 0,6. С учетом уравнения (3) равновесный краевой угол определяется уравнением
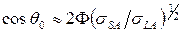 (4)
(4)
Если поверхностное натяжение жидкости 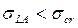 , происходит полное смачивание. При
, происходит полное смачивание. При 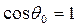 из соотношения (4) следует, что при постоянном значении коэффициента
из соотношения (4) следует, что при постоянном значении коэффициента 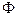 (например, при смачивании одной и той же твердой поверхности различными предельными углеводородами)
(например, при смачивании одной и той же твердой поверхности различными предельными углеводородами) 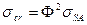 .
.
На основе молекулярной теории удается в ряде случаев предсказывать, как влияют на смачивание некоторые физико-химические факторы, например, размер функциональной группы при смачивании низкоэнергетических твердых тел (полимеров). Работа адгезии пропорциональна потенциальной энергии молекулярного взаимодействия 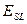 между двумя параллельными поверхностями, которые находятся друг от друга на расстоянии
между двумя параллельными поверхностями, которые находятся друг от друга на расстоянии 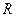 . На основе теории Е.М.Лифшица (1955 г.), энергия взаимодействия плоских поверхностей, которые находятся друг от друга на весьма малых расстояниях, должна уменьшаться обратно пропорционально квадрату расстояния между ними. В рассматриваемом случае
. На основе теории Е.М.Лифшица (1955 г.), энергия взаимодействия плоских поверхностей, которые находятся друг от друга на весьма малых расстояниях, должна уменьшаться обратно пропорционально квадрату расстояния между ними. В рассматриваемом случае 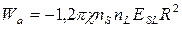 , где
, где 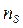 и
и 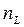 - число молекул твердой и жидкой фаз на единице площади контакта;
- число молекул твердой и жидкой фаз на единице площади контакта; 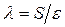 ;
; 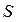 и
и 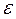 - энтропия и энергия поверхности раздела. Это уравнение позволяет сравнивать краевые углы на разных твердых телах (1 и 2) при контакте с одной и той же жидкостью. В системах с дисперсионным взаимодействием
- энтропия и энергия поверхности раздела. Это уравнение позволяет сравнивать краевые углы на разных твердых телах (1 и 2) при контакте с одной и той же жидкостью. В системах с дисперсионным взаимодействием 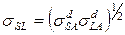 , соответственно
, соответственно 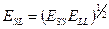 , где
, где 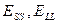 - энергии взаимодействия частиц твердого тела друг с другом и частиц жидкости друг с другом. Отсюда
- энергии взаимодействия частиц твердого тела друг с другом и частиц жидкости друг с другом. Отсюда
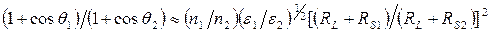
Пусть, например, одна из подложек (1) – углеводород, а другая (2) – фторуглеродное соединение; в качестве смачивающих жидкостей используются иодистый метилен и гексан. Тогда из предыдущего уравнения следует, что различие краевых углов в этом случае обусловлено главным образом различным размером молекул твердого тела. Поэтому для приближенного сравнения смачивания разных полимеров одной и той же жидкостью можно пользоваться соотношением 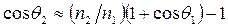 .
.
Улучшение смачивания полимеров при возрастании числа молекул на единицу площади твердого тела наблюдалось во многих случаях. Например, при контакте воды с твердыми предельными углеводородами краевые углы обычно уменьшаются по мере увеличения плотности твердой фазы. На полиэтилене, в котором на 1000 атомов углерода приходится 5 метильных групп, 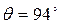 , на полиэтилене с большей степенью разветвленности (21 метильная группа на 1000 атомов углерода) краевой угол возрастает до 101 - 105˚. Аналогичная связь между величиной краевого угла и плотностью твердой подложки наблюдалась при смачивании полиэфиров.
, на полиэтилене с большей степенью разветвленности (21 метильная группа на 1000 атомов углерода) краевой угол возрастает до 101 - 105˚. Аналогичная связь между величиной краевого угла и плотностью твердой подложки наблюдалась при смачивании полиэфиров.
E.Moy and D.Li. Solid/fluid interfacial tensions from contact angles: corroboration by independent approaches //Advances in Colloid and Interface Science 39 (1992) 257-297.
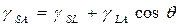 (1)
(1)
Из четырех параметров уравнения Юнга только поверхностное натяжение жидкости 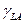 и краевой угол θ могут быть измерены. Чтобы оценить
и краевой угол θ могут быть измерены. Чтобы оценить 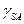 и
и 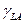 из измерений краевого угла в добавление к уравнению (1) нужно уравнение, включающее три межфазных натяжения (
из измерений краевого угла в добавление к уравнению (1) нужно уравнение, включающее три межфазных натяжения ( 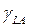 ,
, 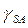 и
и 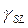 ).
).
Различные уравнения межфазного натяжения, которые можно найти в литературе, можно разделить на две группы: 1) уравнения, основанные на приближении компонентов поверхностного натяжения и 2) уравнения, основанные на приближении уравнения состояния. Есть фундаментальные различия между этими двумя приближениями, которые будут обсуждаться в этой главе детально. Достаточно сказать, что существование уравнения состояния предопределяет возможность уравнений межфазного натяжения, включающих компоненты поверхностного натяжения.
А. Приближение Fowkes:
Концепция компонентов поверхностного натяжения была первоначально предложена Fowkes [10] . Было предположено, что поверхностное натяжение жидкости может быть разложено на компоненты, каждый из которых обусловлен частным типом межмолекулярных сил.
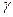 =
= 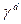 +
+ 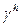 +… (2)
+… (2)
Компоненты 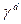 и
и 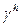 рассматриваются как физические свойства жидкости, называемые дисперсионными компонентом водородных связей поверхностного натяжения, соответственно. Fowkes предполагал, что взаимодействия через поверхность фаз между двумя объемными фазами могут происходить только между силами того же типа, т.е. дисперсионная – дисперсионная, водородная связь – водородная связь. Основываясь на этих предположениях Fowkes предложил уравнение межфазного натяжения (3), применимое к системам, где только дисперсионные взаимодействия являются общими для обеих фаз:
рассматриваются как физические свойства жидкости, называемые дисперсионными компонентом водородных связей поверхностного натяжения, соответственно. Fowkes предполагал, что взаимодействия через поверхность фаз между двумя объемными фазами могут происходить только между силами того же типа, т.е. дисперсионная – дисперсионная, водородная связь – водородная связь. Основываясь на этих предположениях Fowkes предложил уравнение межфазного натяжения (3), применимое к системам, где только дисперсионные взаимодействия являются общими для обеих фаз:
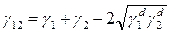 (3)
(3)
Большая часть рассуждений для уравнения (3) исходит из более ранней работы Good et al. [11], которые предположили, что объединенное правило Berthelot для констант притяжения в уравнении Ван дер Вальса может быть использовано для определений межфазных натяжений. Уравнение (3) было развито для систем жидкость – жидкость, однако то же самое уравнение может быть использовано для систем твердое тело – твердое тело и твердое тело – жидкость при условии, что базовый критерий, что только дисперсионные взаимодействия действуют через границу, удовлетворяется (пример: тефлон – вода). Нужно также указать, как сообщают Spelt et al. [12], что «дисперсионные компоненты поверхностного натяжения, определяемые из уравнения (3), не являются материальными свойствами, но являются только функциями общего поверхностного натяжения твердого тела и жидкости».
Fowkes, таким образом, предположил, что правильный путь обращения с недисперсионными взаимодействиями лежит через взаимодействия кислотно-основные [13]. Используя эту новую концепцию, материалы классифицируются как кислоты или основания, согласно концепции Льюиса. Кислоты Льюиса это вещества, имеющие группы с электрон-акцептором, а
основания Льюиса – вещества с группами электрон-донорами. Используя эти определения, например, полиметилметакрилат (ПММА) рассматривается как основное вещество, а поливинилхлорид (ПВХ) – как кислотное. Основываясь на концепции кислотно-основных взаимодействий, Fowkes считает, что поверхностное натяжение твердых тел не может быть измерено из данных краевых углов, и что эта величина может быть получена только из теплот плавления тонко (devided) порошков. Это так, поскольку образование водородных связей, согласно Fowkes – это экзотермическое кислотно-основное взаимодействие, которое ничего не должно делать с диполями. Тем не менее, van Oss et al. [14] вывели уравнение (4) для межфазного натяжения, учитывающее кислотно-основное взаимодействие
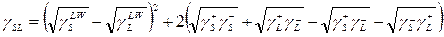 (4)
(4)
Где символ LW представляет Лондон – ван дер Ваальсовский вклад, а символ 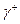 и
и 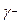 электроноакцепторные (кислота) и электрон-донорные (основание) параметры, которые дают общий кислотно-основный (АВ) вклад в поверхностное натяжение через
электроноакцепторные (кислота) и электрон-донорные (основание) параметры, которые дают общий кислотно-основный (АВ) вклад в поверхностное натяжение через
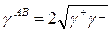 (5)
(5)
Нужно указать, что как в уравнении (4), так и в (5) используются геометрические средние приближения, чтобы представить недисперсионные взаимодействия. Приближение геометрического среднего, как упоминалось выше, происходит из объединенного правила Бертло для констант притяжения в уравнении состояния ван дер Вальса для газов. Это представление, которое имеет некоторое теоретическое обоснование для дисперсионных взаимодействий, не может быть корректным для недисперсионных взаимодействий. Уравнение (4) просто сводится к исходному уравнению Fowkes (3), когда один из материалов (или твердое тело или жидкость) является полностью дисперсионным. Уравнение (3) или (4) в соединении с уравнением Юнга (1) позволяет использовать данные по измерению краевого угла для оценки 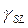 . В упомянутых уравнениях по крайней мере четыре независимых параметра требуются для расчета межфазных натяжений:
. В упомянутых уравнениях по крайней мере четыре независимых параметра требуются для расчета межфазных натяжений: 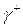 ,
, 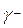 ,
, 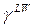 ,
, 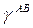 .
.
В. Приближение уравнения состояния
Приближение уравнения состояния для межфазных натяжений основано на предпосылке, что
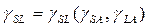 (6)
(6)
Существование уравнения (6) может быть продемонстрировано на термодинамической основе, используя два приближения: отношения Гиббса – Дюгема [15], кА было исходно сделано, и позднее из рассмотрения правила фаз [16], которое коротко обсуждено ниже. Подробное формулирование уравнения (6) вместе с уравнением Юнга в этом случае позволит рассчитать 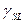 по краевому углу.
по краевому углу.
Число степеней свободы в системе, пренебрегая вкладом от поверхностей и линий, дается правилом фаз Гиббса. Набор интенсивных переменных, который полностью описывает состояние для объемных систем, состоит из температуры, Т, давления, Р, и мольных долей x. Для n независимых компонентов имеется n – 1 независимых переменных x. Так, для системы, подразумевающей n независимых компонентов в p фазах, число независимых переменных интенсивных свойств, т.е. число степеней свободы f дается
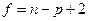 (7)
(7)
Так, физическое состояние, например, воды в стакане в равновесии с ее паром (n =1, p = 2) полностью определяется, если одна интенсивная переменная известна. Для системы, состоящей из капли воды, окруженной ее паром, число степеней свободы все еще будет 1, согласно (7). Однако, хорошо известно из эксперимента, что и температура и давление могут использоваться как независимые переменные; число степеней свободы должно быть равно двум.
Применение правила фаз Гиббса к искривленным поверхностям и системам, где вклады поверхности существенны, приведет к неправильным величинам для числа степеней свободы [16]. Если уравнение (7) используется для двухкомпонентной системы твердое тело – жидкость – газ (сидячая капля), число степеней свободы должно быть равно
n = 2, p = 3,
f = 2 – 3 + 2 =1,
Что привело Джонсона [17] к ошибочному выводу, что уравнение состояния для межфазных натяжений не может существовать. Правильное правило фаз для систем, где эффекты поверхности и линии важны, как для системы, обсуждавшейся в предыдущем разделе, было получено Li et al. [16]. Для систем, которые включают умеренно искривленные поверхности, набор интенсивных переменных состоит из T,P и x, как для объемных, так и для поверхностных фаз, вместе с межфазными натяжениями 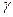 . Для таких систем число механических связанных уравнений (constraint) уравнений обычно меньше, чем для только объемных систем, следовательно, число степеней свободы возрастет. Например, уравнение Юнга (1) – уравнение механического равновесия, но не является связывающим уравнением, поскольку краевой угол θ не принадлежит к набору интенсивных переменных. Обобщенное правило фаз тогда
. Для таких систем число механических связанных уравнений (constraint) уравнений обычно меньше, чем для только объемных систем, следовательно, число степеней свободы возрастет. Например, уравнение Юнга (1) – уравнение механического равновесия, но не является связывающим уравнением, поскольку краевой угол θ не принадлежит к набору интенсивных переменных. Обобщенное правило фаз тогда
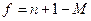 (8)
(8)
Где М – число Р1=Р2 типа связанных уравнений, где индексы 1 и 2 представляют разные фазы.
Применение уравнения (8) к двухкомпонентной системе (твердое тело и жидкость), состоящей из сидячей капли на гомогенной и изотропной твердой подложке дает
n = 2 и М = 1 ( 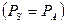
и 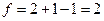
Следовательно, из обобщенного уравнения правила фаз (8) система имеет 2 степени свободы, указывая, что уравнение в форме уравнения (6) существует.
Точное формулирование уравнения (6) пока не было сделано аналитически. Имеются, однако, эмпирические уравнения состояния, из которых только уравнение Неймана было широко использовано и проверено [8]. Уравнение состояния было основано на данных краевого угла на низкоэнергетических поверхностях и имеет следующую форму
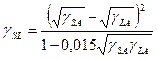 (9)
(9)
Позднее было предложено уравнение в форме
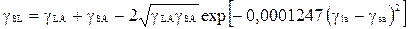
МОЛЕКУЛЯРНЫЕ МЕХАНИЗМЫ ОПУХОЛЕВОГО РОСТА
В последние десятилетия достигнут значительный прогресс в выяснении молекулярных механизмов канцерогенеза. Идентифицированы генетические дефекты, определяющие необходимые и достаточные свойства раковой клетки: постоянную митогенную стимуляцию, нечувствительность к антиростовым и проапоптотическим сигналам, неограниченный пролиферативный потенциал, способность индуцировать ангиогенез, инвазию и метастазирование. Сформулировано представление о многостадийности (многоступенчатости) канцерогенеза, как процесса накопления в клетке генетических дефектов, вызывающих дискретные и необратимые изменения ее генотипа. Выявлены функциональные связи опухоли с нормальным окружением и установлена поразительная способность раковых клеток рекрутировать окружающие здоровые ткани для стимуляции собственного роста и прогрессии. Определены механизмы злокачественной инвазии и метастазирования и уточнена роль в этих процессах адгезивных взаимодействий опухолевых клеток друг с другом и с внеклеточным матриксом. Совершенствуются методы диагностики опухолей, основанные на определении опухолевых антигенов и онкофетальных белков. Разрабатываются принципиально новые молекулярно-биохимические подходы к терапии рака.
Вышеизложенное диктует настоятельную необходимость обобщения современных представлений об опухолевом росте и его молекулярных механизмах, позволяющего помочь студенту разобраться в основных проблемах канцерогенеза, понять смысл и следствие новых событий в онкологии, а главное – подготовить его к восприятию новых научных идей. Мы полагаем, что решению этой задачи поможет настоящее пособие, содержащее иллюстративный материал, сопровождаемый лаконичными пояснениями.
Знакомство с пособием, несомненно, предполагает достаточную подготовленность читателю по ряду вопросов в области биохимии, генетики, нормальной и патологической физиологии, цитологии – положение, наглядно демонстрирующее необходимость интеграции знаний по важнейшим медико-биологическим дисциплинам.
Пособие снабжено тестовыми заданиями и вопросами, обеспечивающими возможность самоконтроля знаний.
Дата добавления: 2015-03-26; просмотров: 1021;
