Параллельные краевые дислокации

Взаимодействие двух параллельных краевых дислокаций сложнее из-за отсутствия симметрии (рис.21). Силы, действующие в их параллельных разведенных на расстоянии h плоскостях скольжения:

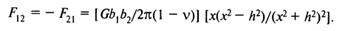
следуют из выражения для касательных напряжений:

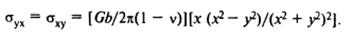
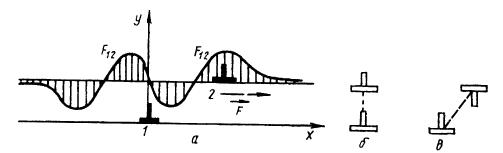
Рисунок 21. Взаимодействие двух параллельных краевых дислокаций: а – зависимость силы от расстояния x между ними; б, в – устойчивые положения одноименных (б) и разноименных (в) дислокаций (диполь).

При |x|®¥ сила F®0 (на бесконечности взаимодействия нет). Есть три корня F(x)=0 в точках x=0 и x=±h и четыре экстремума с координатами x_1,2,3,4= 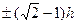, в которых сила достигает максимума. Для одноименных дислокаций одно положение при x=0 устойчивое (рис. 21б), когда при малых отклонениях от нуля сила 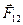возвращает дислокацию к положению x=0, и два неустойчивых. Группа дислокаций, расположенных друг под другом в положении устойчивого равновесия образуют устойчивую систему многих дислокаций в кристалле – стенку дислокаций. У разноименных дислокаций неустойчивым является одно положение x=0.

Чтобы вывести краевую дислокацию из устойчивого равновесия в x=0 надо преодолеть барьер в точке 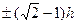, приложив в плоскости скольжения напряжение:

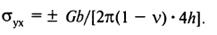
У разноименных дислокаций устойчивых положения два: x=±h (под углом 45°).Две разноименные дислокации в положении устойчивого равновесия образуют дислокационный диполь (рис. 21в). Для расцепления диполя требуется то же напряжение, что и для стенки дислокаций.

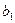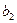Параллельные краевая и винтовая дислокации не взаимодействуют никак – в их полях нет ни одной общей компоненты. В общем случае параллельных смешанных дислокаций с векторами Бюргерса и , образующими углы j₁ и j₂, соответственно, с направлением их осей 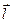║ ║ 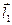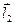суммируются силы парного взаимодействия 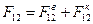, вычисленные отдельно для винтовых компонентов с векторами Бюргерса 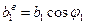, 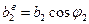и краевых компонентов , .

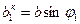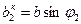Общий закон взаимодействия для параллельных дислокаций в одной плоскости скольжения (h=0): одноименные дислокации отталкиваются, разноименные – притягиваются. Для краевых дислокаций в разных плоскостях закон взаимодействия сложнее – он зависти от взаимного расположения и расстояния между ними.