Сила, действующая на дислокацию

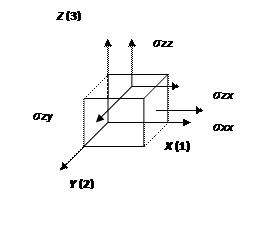
Рисунок 16. Нормальные и касательные напряжения в координатах базиса решетки

(x [100], y [010], z [001])

Приложенное к кристаллу извне напряжение σ_ij создает в плоскости скольжения дислокации 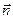в направлении ее вектора Бюргерса 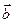напряжение

,

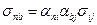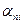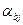где и - направляющие косинусы между кристаллографическими направлениям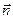и 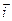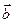и ; и .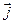

Индексы x или 1, y или 2, z или 3 соответствуют кристаллографическим индексам в базисе решетки: [100], [010], [001].

Например, если напряженное состояние задано единственной компонентой тензора σ₁₁ или σ_xx, то в плоскости скольжения дислокации 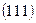в направлении ее вектора сдвига 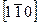будет действовать касательное (сдвиговое) напряжение:

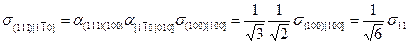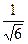= σ_xx.

Это напряжение создает силу, действующую на дислокацию, которая описывается модулем силы = 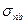b∙или F=τ_n b и единичным вектором .

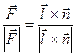Сила зависит от вектора Бюргерса, а не от вектора оси, поэтому в любой точке оси дислокации 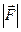=const и направлена по нормали к оси дислокации (рис. 17).

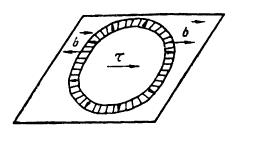
Рисунок 17. Внешние силы, действующие на петлю дислокации в плоскости 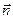, где приложено постоянное касательное напряжение τ.

Под действием касательного напряжения в плоскости петли она расширяется. Работа пластического сдвига заключается в расширении площадки сдвига, очерченной дислокацией.