Рівняння неперервності
Це рівняння зв’язує густину з характеристиками руху суцільного середовища, що встановлюється на основі закону збереження маси (повна зміна маси у замкненому об’ємі дорівнює нулю)
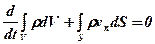 ,
,
де перша складова характеризує зміну маси в довільно вибраному об’ємі V, а друга – масу середовища, що притікає або відтікає через поверхню І за одиницю часу (vn –проекція швидкості на нормаль до поверхні S).
У диференціальній формі рівняння неперервності має такий вигляд:
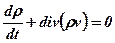 . (5.18)
. (5.18)
Для твердих деформованих тіл у випадку, коли компоненти неперервного поля переміщень задані, за рівнянням Коші (5.6) можна визначити компоненти поля деформацій. Складніше з постановкою оберненої задачі – визначення переміщень за деформаціями. Не для кожного поля деформацій існує неперервне поле переміщень. Деформації, яким відповідає неперервне поле переміщень, називаються сумісними деформаціями. В іншому випадку деформації вважаються несумісними.
Необхідною умовою сумісності деформацій є їх відповідність геометричним рівнянням сумісності, які одержують безпосередньо з рівнянь Коші:
 (5.19)
(5.19)
Ці рівняння забезпечують, по суті, суцільність деформованого твердого тіла і називаються також рівняннями суцільності, або неперервності.
Рівняння енергії
Це рівняння відображає закон збереження енергії для суцільного середовища і є наслідком фундаментального закону фізики – першого начала термодинаміки. У диференціальній формі рівняння енергії при відсутності джерел теплоти має вигляд
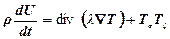 , (5.20)
, (5.20)
де U – питома (віднесена до одиниці маси) внутрішня енергія суцільного середовища;
Т – температура;
l – коефіцієнт теплопровідності суцільного середовища.
Система рівнянь (5.16), (5.18), (5.20) представляє необхідні фундаментальні рівняння руху суцільного середовища
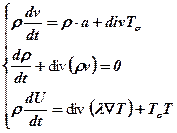
Дата добавления: 2015-03-20; просмотров: 897;
