Рівняння руху
 |
Ці рівняння для довільного об’єму V суцільного середовища, обмеженого замкнутою поверхнею S (рис. 5.5), базуються на використанні принципу д’Аламбера.
 |
У загальному випадку на даний об’єм діють:
об’ємні сили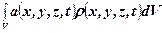 
з вектором прискорень а,
поверхневі сили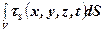 
з вектором напружень tS ,
сили інерції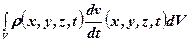 
з вектором прискорень 
,
де 
– густина середовища.
Вектор напружень визначається через компоненти тензора напружень (5.1)
,
де i, j, k – орти декартової системи координат.
Рівняння руху суцільного середовища визначаються з умов рівності нулю головного вектора та головного моменту всіх сил і в інтегральній формі мають вигляд
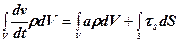; (5.14)
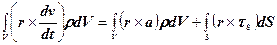, (5.15)
де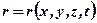 
–радіус-вектор точки у вибраній системі координат (рис. 5.5)
Рівняння (5.15) вказує на симетрію тензора напружень (5.1), і апріорі приймаючи симетрію Тs , можна його не використовувати.
Рівняння (5.14) у векторній диференціальній формі матиме вигляд
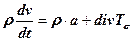. (5.16)
Похідна 
характеризує зміну швидкості матеріальної точки суцільного середовища, що переміщується у просторі і називається субстанційною похідною.
Вона визначається як
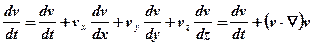, (5.17)
де 
– операція Гамільтона.
Перший доданок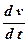 
називається локальною похідною і характеризує зміну швидкості у фіксованій точці простору з часом, а другий доданок 
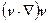– конвективною похідною і характеризує зміну швидкості при переміщенні з однієї точки в іншу.
Дата добавления: 2015-03-20; просмотров: 527;