Напруження і деформації суцільних середовищ

Суцільне середовище – це гіпотетичне середовище, яке може під дією навантажень як завгодно змінювати свою форму (деформуватись), не втрачаючи при цьому суцільності.

Методи механіки суцільних середовищ широко застосовують в інженерній практиці для розрахунків і прогнозування напруженого стану та деформацій твердих тіл, течій рідин, газів та їх сумішей і т. ін.

Зовнішні сили, які діють на тіло (середовище), що розглядається, поділяються на поверхневі та об’ємні.

Поверхневі сили виникають внаслідок контакту тіла із зовнішнім середовищем і всередині суцільного середовища відповідно до третього закону Ньютона врівноважуються. Це сили тиску, тертя, взаємодії і т. ін. Вони можуть бути розподіленими і зосередженими.

Об’ємні сили – це результат дії на середовище просторового векторного поля. Об’ємні сили неперервно розподілені у середовищі. Це сили інерції, гравітаційні сили і т. ін.

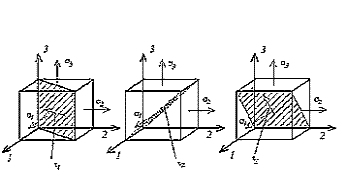
При дії зовнішніх сил міх окремими частинками суцільного середовища виникають сили взаємодії, які називаються внутрішніми силами. Вони визначають напружений стан суцільного середовища, який характеризується дев’ятьма компонентами напружень (рис 5.1).

Напруження, перпендикулярні до граней куба, називаються нормальнимиі позначаються 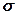, а ті, що діють в площині грані – дотичними і позначаються τ з відповідними індексами.

Ці напруження, складені у формі матриці, визначають тензор напружень.

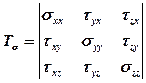, (5.1)

Тензор напружень є симетричним відносно головної діагоналі.

У кожній точці суцільного середовища існують такі взаємно перпендикулярні площадки, на яких дотичні напруження

Відповідні напруження 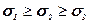є головними нормальними напруженнями, які утворюють тензор

.

У перерізах, що порівну розділяють кути між головними площинами і проходять через головні осі 1, 2 та 3 (рис. 5.2), дотичні напруження досягають екстремальних значень і називаються головними дотичними напруженнями:

; : .

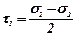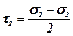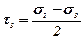Головні нормальні напруження s_і (і=1,2,3) є коренями кубічного рівняння

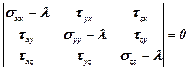
або

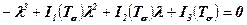. (5.2)

Оскільки нормальні напруження не залежать від вибору координатної сітки, то, очевидно, коефіцієнти кубічного рівняння (5.2) не залежать від вибору системи координат. Ці коефіцієнти, які записані на головних осях

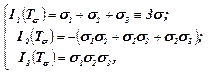
називаються відповідно лінійним (першим), квадратичним (другим), і кубічним (третім ) інваріантами тензора напружень.

Величина називається середнім, або гідростатичним тиском у даній точці.

Тензор напружень можна представити у вигляді суми

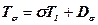, (5.3)

де Т₁ - одиничний тензор;

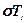– кульовий (сферичний) тензор, що відповідає середньому тиску в даній точці;

– тензор, що визначає дотичні напруження в даній точці і називається девіатором напружень.

Девіатор напружень характеризується головними напрямками, які збігаються з напрямками тензора напружень, а головні значення напружень девіатора дорівнюють .

Інваріанти девіатора напружень визначаються за системою

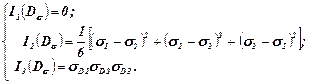(5.4)

Величина

(5.5)

називається інтенсивністю дотичних напружень.