Прямые измерения с однократными наблюдениями

За результат измерения в этом случае принимают результат однократного наблюдения Х (с введением поправки, если она имеется), используя предварительно полученные (например, при разработке МВИ) данные об источниках, составляющих погрешность.

Подавляющее большинство измерений - однократные. Вообще, в бытовой практике людей, в производственной практике выполняются однократные измерения (токарная обработка, фрезерная обработка, кузнечно-штамповое производство, сборка машин, слесарно-лекальная обработка деталей и т.д. исключая тонкую настройку или прецизионные сопряжения деталей). Иногда, в отдельных случаях, применяют два или три метода измерений, взаимоисключающих погрешности. В обычных условиях точность однократных измерений вполне приемлема, а простота, высокая производительность - (количество измерений в единицу времени и сравнительно низкая стоимость по оценке трудозатрат) ставят их вне конкуренции. Если, человек задался вопросом о том, что такое однократные и многократные измерения, то возникает другой вопрос: - почему в теории и практике измерений столько сложностей, формул, чуть ли не «миф» такой научности и невозможности избавиться от какой-то там погрешности? В жизни нашей, в быту, в магазине, на работе, мы редко имеем прямое ощущение погрешности при измерениях и постепенно привыкаем к тому, что этих погрешностей нет в природе, а метрологи их просто придумывают, чтобы оправдать свою занятость! На самом-то деле погрешность существует всегда, но мы ее или не учитываем, или ее величина настолько незначительная, что ею можно пренебречь, но, в любом случае, при измерениях мы обязаны ее оценить, хотя бы на примерном уровне, а затем количественно. Пренебрежение этой погрешностью в жизни людей часто мстительно «аукается» тем кто ей пренебрегает. Хотя, имея такой опыт, мы опять и опять «наступаем на эти грабли» и до конца своей жизни не понимаем или не сталкиваемся с обстоятельствами, требующими более точного подхода к измерениям, и применяем только однократные измерения. Не ошибается, или ошибается, но значительно реже, лишь тот, кто относится к любым измерениям, как к случайному событию измерительного наблюдения и не считает результат наблюдения за окончательный результат измерения. Проводит еще два наблюдения и, после элементарного анализа и осмысления на априорность полученной информации, по величине наблюдения и погрешности, делает окончательный расчет результата измерения, хотя бы на глаз, на вскидку. Итак, необходимым условием проведения однократного измерения служит наличие априорной информации о количестве физических величин, какого - либо параметра. Что значит «априорная»?! Это значит - примерная, на глаз вам уже известная информация. Например: Длина стола; Величина напряжения переменного тока; Величина температуры горящего пламени в топке котла, и т.д. Вам с достаточно высокой точностью уже известно или видно, из опыта предыдущих измерений, с какой вероятностью (вид закона распределения случайных событий) результаты наблюдений дают ожидаемый результат измерения, после простейших операций расчетной оценки. Кроме этой информации, при сомнении, Вы можете дополнительно использовать информацию о том, насколько результат наблюдения отличается от нормируемого результата (параметра, размера) по НТД, о классе точности средства измерения, которым Вы воспользовались, и величине поля допуска (квалитета) нормируемого размера. В болшинстве случаев в жизни любого человека все эти рассуждения выполняются на подсознательном уровне почти автоматически и не приходят в ум до тех пор, пока не произойдёт какое либо «ЧП» и вот тогда, обжёгшись, человек начинает понимать, что всё существует наяву, но не осознаётся как бы на бегу поспешности жизни. В связи с этим Вам необходимо, под «флагом» метрологической экспертизы, провести анализ соответствия цены деления СИ, его класса точности с величиной поля допуска и их соотносительности по сравнительным величинам. Поле допуска может быть симметричным - плюс, минус «А» или плюс А1, минус А2. В зависимости от класса точности и чувствительности СИ Вы будете иметь величину цены деления – «В». Соотношение - плюс, минус А или (А1 - А2) к «В» должно быть много больше единицы (лучше всего 5 и выше), т.е. величина цены деления СИ должна укладываться в поле допуска как минимум один раз или больше. Из этого Вам нужно учесть величины поправок - аддитивных и мультипликативных (от латинских слов addituvus - прибавляемый, multiplico - умноженный). Эти поправки, как правило неизвестны, но если проводятся 3 наблюдения при измерениях и есть их различия по величине – Х_max. и Х_min., то в Вашем случае поправки существуют и следует оценить норму однократности измерений. К такой норме относится известная зависимость (9.14, 9.15, 9.16)

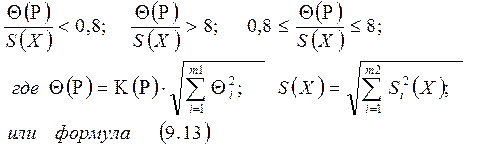
где К(Р) – коэффициент, определяемый принятой Р(х) и числом m1;

Qj – найденные нестатическим методами границы j-й составляющей НСП (неисключенным остатком систематических погрешностей), представляющей границы интервала, внутри которой находится эта составляющая, определяемые при отсутствии сведений о вероятности ее нахождения в этом интервале. Значения К(Р) берется по таблице 9.2;

S (x) - СКО, среднеквадратическое отклонение случайных величин.

Допустим, у Вас получены 3 наблюдения измерений - X_max, X_i, X_min Граница доверительной вероятности размаха результатов наблюдений X_max -X_min. Необходимо сравнить величину этой границы с величиной поля допуска в НТД, сколько раз вмещается эта граница в величину поля допуска? Если вмещается как минимум один раз с вероятностью 0,99 или 1,0, то априорная информация обеспечивается на 100 % и однократность измерения обеспечивается. Если этого оценить сразу нельзя, то делается расчет вышеуказанной зависимости.

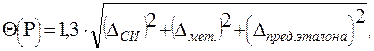
при N ≥ 4 составляющих НСП получаем НСП - неисключенный остаток систематической погрешности, от которой нельзя избавиться.

S (X) -среднеарифметическое от наблюдений = å(Xmax. +Xi+Xmin.)/3;

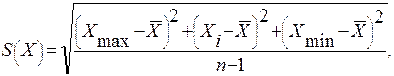
получаем СКО = S(x).

Делим Qi на S(x), если результат больше или равен 8, то однократные измерения имеют право на осуществление и тогда суммарная погрешность намного меньше цены деления СИ и поля допуска, пренебрегают случайной погрешностью СКО и принимают D(Р) = Qi(P). В этих случаях Методика Выполнения Измерений по ГОСТ Р 8.563 - 96 может быть совмещена с инструкцией на эксплуатацию СИ и норму, заложенную в НТД - ( КД, ТД и технологическую инструкцию).

Если Qi(Р)/S(x)< 0,8, то величиной Qi(Р) - НСП пренебрегают и окончательно принимают за погрешность результата измерения

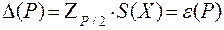
при доверительной вероятности (Р).

где Z1,2 - коэффициент Лапласа по спец. таблицам от вероятности (Р).

Если 0,8 < Qi(P)/S(x) < 8, то доверительную границу погрешности результата измерений вычисляют по формуле (9.12). В таких случаях необходимо провести с результатами наблюдений при измерениях строгий статистический перерасчет погрешности, границы доверительной вероятности и т.д. с обязательными процедурами по Методике Выполнения Измерений (МВИ) по ГОСТ Р 8.563 - 96 и ее документированием. Процедуры перерасчета имеют большой объем и в краткой форме здесь приведены быть не могут. Желающим необходимо обратиться к специальной метрологической литературе. За результат измерения в любом случае принимается выражение: <Аi - e(P)> меньше или равно «А» меньше или равно <Аi + e(P)>; где: e(Р) погрешность в зависимости от того, какими величинами можно пренебречь, а какие подлежат обязательному учету.

Из методического материала в помощь метрологам - Москва, ТОО «ТОТ» 1996 год. по МВИ ГОСТ Р 8.563 - 96 - стр. 6-7 следует: «Наиболее часто, на практике в качестве исходных данных для установления требований к точности измерений при контроле используют допуск на контролируемый параметр (Квалитет). Считается удовлетворительным соотношение между пределом погрешности измерений и границей симметричного поля допуска - 1:5, в ряде случаев - 1:4. При соотношении - 1:3 вводится контрольный (суженый) допуск на контролируемый параметр. Иногда требования точности измерений устанавливают в виде пределов допускаемых значений характеристик абсолютной или относительной погрешности измерений. Форма приведенной погрешности измерений не используется - (это одна из форм выражения погрешности средств измерений - СИ, которая достаточно всем известна.) Наиболее распространенным способом выражения требований к точности измерений является граница допускаемого интервала наблюдений при измерениях, в котором с заданной вероятностью «Р» должна находиться погрешность измерения, т.е. вышеуказанная зависимость соотношений НСП и СКО. Такое соотношение часто иллюстрируется формулой коэффициента точности – К_т = ׀1/2 Т_е׀/Δ_си = 5:1; 4:1; 3:1(суженый). Если границы симметричны, то перед их одним числовым значением ставят знак ±e(Р) - поправка к среднеарифметическому значению наблюдений при измерениях и это будет являться результатом измерений. Если «Р=1», то требований к точности измерений используются именно эти пределы допускаемых значений погрешностей измерений – «e(Р)=D», при этом вероятность «Р=1» не указывается». На основании этой выдержки из ГОСТ Р 8.563 - 96 - стр.4, не все МВИ необходимо регламентировать документально самостоятельно, разрабатывать текст МВИ - ее содержание и аттестацию строго по ГОСТ Р 8.563 - 96 не обязательно, особенно для измерений давления, с помощью показывающих манометров, электрических величин щитовыми приборами, линейно-угловых и многих других величин, подпадающих под вышеприведенные зависимости, с помощью простых средств измерений - СИ. В этих случаях МВИ не нужно оформлять отдельным документом по ГОСТ Р 8.563 - 96, а достаточно указаний в КД, ТД, Проектной документации на крупный объект технологического оборудования без сложных измерительных зависимостей, инструкций по использованию СИ или ТУ на СИ, оформленные соответствующим стандартом, зарегистрированных в Госреестре типа СИ. Однако, там где требуется определять сложные функциональные зависимости при испытаниях продукции или его изготовлении - (аэродинамические, тепловые испытания машин, расхода газожидкостных материалов и т.п.), то МВИ необходимо оформлять по ГОСТ Р 8.563 - 96, в ТУ на сложную продукцию также необходимо включать МВИ с указанием их регистрационных номеров, после их аттестации в порядке установленным ГОСТ Р 8.563 - 96. Необходимо иметь в виду тем, кто не знает о том, что Госстандарт РФ силами своих институтов ведет работу по разработке МВИ распространенного типа, что эти МВИ появляются в печати под следующим видом: - После цифры 563 в таких МВИ стоит точка и новая цифра - порядковый номер такой МВИ, например - ГОСТ Р 8.563.3 - 97 «ГСИ. Измерение расхода и количества жидкостей и газов методом переменного перепада давления. Процедура и модуль расчетов. Программное обеспечение». Таким образом, понимание однократных наблюдений при измерениях к оператору (человеку) приходит только после тщательного осознания технологии многократных наблюдений при измерениях, хотя в РМГ 29 - 99 записано, что однократные измерения это такие измерения, которые выполняются один раз!