Косвенные измерения при линейной зависимости

Искомая величина А связана с m измеряемыми аргументами уравнением (9.16) /5/

(9.16)

где b_i - постоянные коэффициенты.

Предполагается, что корреляция между погрешностями измерений a_i отсутствует.

Результат измерения `А вычисляют по формуле (9.17) /5/

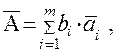(9.17)

где `а_i - результат измерения а_i с введенными поправками.

Оценку СКО результата измерения S (`A) вычисляют по формуле (9.18) /5/

(9.18)

где S²(ā_i) - оценка СКО результата измерений ā_i .

Доверительные границы e (Р) случайной погрешности `А при нормальном распределении погрешностей `аi вычисляют по формуле (9.19) /5/

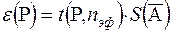, (9.19)

где t(P,n_эф) - коэффициент Стьюдента, соответствующий доверительной вероятности Р (обычно 0,95 , в исключительных случаях 0,99) и эффективному числу наблюдений; – n_эф, вычисляемому по формуле (9.20)

(9.20)

где n_i - число наблюдений при измерении а_i.

Доверительные границы Q(Р) НСП результата такого измерения, сумму Q (Р) и e(Р) для получения окончательного значения D(Р) рекомендуется вычислять с использованием критериев и формул (2,3,9 - 11), в которых m1,Qi,и S(x) заменяются, соответственно, на m, bi,Qi, и S(`A).