Прямые измерения с многократными наблюдениями
Рассмотрим группу из «n» независимых результатов наблюдений случайной величины X , подчиняющейся нормальному закону распределения случайности событий при измерениях.
Доверительные границы НСП результата измерения QI (Р) вычисляют по формуле (9.1) /5/
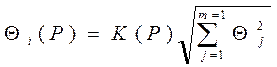 , (9.1)
, (9.1)
где К (Р) - коэффициент, определяемый принятой Р и числом m1 или N, согласно РМГ 29 – 99, составляющих НСП;
Θj - найденные нестатистическими методами границы j-ой составляющей НСП (границы интервала, внутри которого находится эта составляющая, определяемые при отсутствии сведений о вероятности ее нахождения в этом интервале)
при Р = 0,90 К(Р) = 0,95 , при Р = 0,95 К(Р) = 1,1 соответственно при любом числе слагаемых mi.
Далее значения сведены в таблицу 9.1.
Таблица 9.1 - Значения К (Р) от m1 при Р = 0,99
| При Р = 0,99 значения К(Р) | |
| m1 | К(Р) |
| 1,2 | |
| 1,3 | |
| 1,4 | |
| 1,45 | |
| 1,45 |
Если составляющие НСП распределены равномерно и заданы доверительными границами Θj (Pj), то доверительную границу НСП результата измерения вычисляют по формуле (9.2) /5/
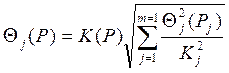 , (9.2)
, (9.2)
где К(P) и Кj - те же, что и в предыдущем случае, коэффициенты, соответствующие доверительной вероятности Р и Рj соответственно;
mj - число составляющих НСП.
Этими действиями анализируется применяемые СИ.
Далее приступают к обработке случайной погрешности по результатам наблюдений.
Обработку результатов в этом случае рекомендуется начать с проверки на отсутствие промахов (грубых погрешностей). Промах - это результат Хn отдельного наблюдения, входящего в ряд из n наблюдений, который для данных условий измерений резко отличается от остальных результатов этого ряда. Если оператор в ходе измерения обнаруживает такой результат и достоверно находит его причину, он вправе его отбросить и провести (при необходимости) дополнительное наблюдение взамен отброшенного.
При обработке уже имеющихся результатов наблюдений произвольно отбрасывать отдельные результаты нельзя, так как это может привести к фиктивному повышению точности результата измерения. Поэтому применяют следующую процедуру. - вычисляют среднее арифметическое `Х результатов наблюдений Хi по формуле (9.3) /5/
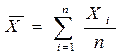 , (9.3)
, (9.3)
Затем по формуле (9.4) вычисляют оценку СКО результата наблюдения /5/
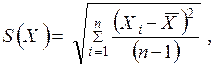 (9.4)
(9.4)
По формуле (9.5) находят отклонение nn предполагаемого промаха Хn от `Х /5/
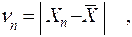 (9.5)
(9.5)
По числу всех наблюдений n (включая Хn) и принятому для измерения значению Р (обычно 0,95) по таблице 9.2 – находят Z(P,n) = 1,96 - значение Лапласа - нормированное выборочное отклонение нормального распределения. Если nn < Z(P,n)× S(X), то наблюдение Xn не является промахом; если nn ³ Z(P,n) × S(X), то Xn - промах, подлежащий исключению. После исключения Xn повторяют процедуру определения `Х и S(X) для оставшегося ряда результатов отклонений от нового значения `X (вычисленного исходя из (n - 1)). Почему (n – 1), а не n мы рассматривать не будем, т.к. это вопрос теоретической метрологии. За результат измерения принимают среднее арифметическое `Х результатов наблюдений Хn. Погрешность Хi содержит случайную и систематическую составляющие. Случайную составляющую, характеризуемую СКО результата измерения, оценивают по формуле (9.6) /5/
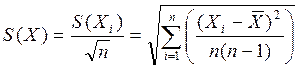 , (9.6)
, (9.6)
В предположении принадлежности результатов наблюдений Xi к нормальному распределению, находят доверительные границы случайной погрешности результата измерения при доверительной вероятности Р по формуле (9.7) /5/
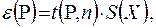 (9.7)
(9.7)
где t - коэффициент Стьюдента.
Таблица 9.2 - Значения t при P равной
| n | Р=0,70 | Р=0,90 | Р=0,95 | Р=0,997 |
| 1,963 | 6,314 | 12,706 | 212,2 | |
| 1,386 | 2,920 | 4,303 | 18,216 | |
| 1,250 | 2,353 | 3,182 | 8,891 | |
| 1,190 | 2,132 | 2,776 | 6,435 | |
| 1,156 | 2,015 | 2,571 | 5,376 | |
| 1,134 | 1,943 | 2,447 | 4,800 | |
| 1,119 | 1,895 | 2,365 | 4,442 | |
| 1,108 | 1,860 | 2,306 | 4,199 | |
| 1,100 | 1,833 | 2,262 | 4,024 | |
| 1,076 | 1,761 | 2,145 | 3,583 |
Доверительные границы (Р) НСП результата измерения с многократными наблюдениями определяют точно так же, как и при измерении с однократным наблюдением - по формулам (9.2) или (9.3).
Суммирование систематической и случайной составляющих погрешности результата измерения при вычислении (Р) рекомендуется осуществлять с использованием критериев и формул (9.9), (9.10) и (9.11), в которых при этом S(X) заменяется на
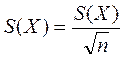
СКО результата измерения с однократным и многократным наблюдением вычисляют одним из следующих способов:
1.Если в технической документации на СИ или в МВИ, указаны нормально распределенные составляющие случайной погрешности результата наблюдения (инструментальная, методическая, из-за влияющих факторов, оператора и т.д.), то СКО вычисляют по формуле (9.9) /5/
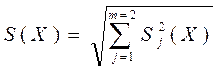 , (9.9)
, (9.9)
где m2 - число составляющих случайной погрешности;
Sj - значения СКО этих составляющих.
Доверительную границу случайной погрешности результата измерения
e (Р) в этом случае вычисляют по формуле (9.10) /5/
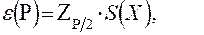 (9.10)
(9.10)
где Zp/2 - значение нормированной функции Лапласа в точке р/2 при доверительной вероятности Р приведены в таблице 9.3.
Таблица 9.3. - Значения функции Лапласа от Р
| Р | Zp/2 |
| 0,90 | 1,65 |
| 0,95 | 1,96 |
| 0,96 | 2,06 |
| 0,97 | 2,17 |
| 0,98 | 2,33 |
| 0,99 | 2,58 |
2. Если в тех же документах случайные составляющие погрешности результата наблюдения представлены доверительными границами ej (Р) при одной и той же доверительной вероятности Р , то доверительную границу случайной погрешности результата измерения при доверительной вероятности Р вычисляют по формуле (9.11) /5/
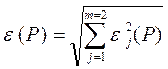 , (9.11)
, (9.11)
3. Если случайные составляющие погрешности результата наблюдения определяют предварительно в реальных рабочих условиях экспериментальными методами при числе наблюдений nj < 30, то доверительную вероятность Р вычисляют по формуле 9.12 /5/
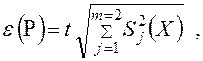 (9.12)
(9.12)
где t - коэффициент Стьюдента, соответствующий наименьшему числу наблюдений n min из всех n;
Sj(X)-оценки СКО случайных составляющих погрешности результата наблюдения, определяемых по формуле (9.13), на отсутствие промахов.
Если в эксперименте невозможно или нецелесообразно определить СКО составляющих случайной погрешности и определенно сразу суммарное СКО, то в формуле (9.7) доверительной границы 3-го случая m 2 = 1.
4. Если случайные составляющие погрешности результата наблюдений представлены доверительными границами (Р), соответствующими разным Р, то сначала определяют СКО результата измерения по формуле (9.13) /5/.
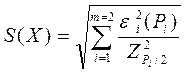 , (9.13)
, (9.13)
Затем вычисляют e (Р) по той же формуле (9.5) первого случая, где Zp/2 - значения функции Лапласа.
Z
S(X) - С К О отдельных наблюдений.
На основании нижеследующей оценки делается вывод о количестве наблюдений - однократные или многократные измерения.
Для суммирования систематической и случайной составляющей погрешностей рекомендуется следующий способ /5/.
Если
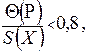 (9.14)
(9.14)
то НСП Q(Р) пренебрегают, так как она стремится к нулю и окончательно принимают Є(Р) за погрешность результата измерения D(R) при доверительной вероятности Р. Таким образом D(R) = Є(Р) = Zp/2 · S(X);
Если Qi (P) / S(X) > 8 , то измерения являются, как правило, однократными (QI (P) - граница НСП результата измерений). Таким образом,
если:
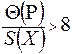 , (9.15)
, (9.15)
то пренебрегают случайной погрешностью СКО – S(X), которая стремится к нулю, и принимают D (Р) = Q (Р). Это характеризуется высокой точностью выбора средства измерения с включением его в технологисекий процесс и применяется в основном в технологиях массового производства продукции на каждом рабочем месте, а также контролируется службами ОТК и СМК.
Если соотношение НСП и СКО будут иметь такой интервал:
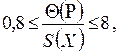 (9.16)
(9.16)
то доверительную границу погрешности результата измерений вычисляют по следующей комплексной формуле (9.17) /5/
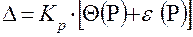 , (9.17)
, (9.17)
где
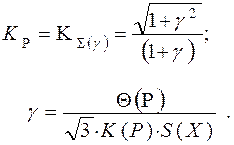
В квадратных скобках К(Р), при определении величины «γ» принимается по таблице 9.4 от формулы (9.2).
По вычисленному значению в приведенной таблице находят значения
Если вычисленные по формуле и таблице значения КΣ(γ), не совпадают, то проводят эстрополяцию между этими значениями.
Таблица 9.4 - Значения KS(g) от показателя γ
| g | 0,3 | 0,5 | 0,7 | 1,0 | 1,5 | 2,0 | 3,0 | 4,0 | 5,0 | ¥ | |
| KS(g) | 1,00 | 0,8 | 0,75 | 0,7 | 0,71 | 0,7 | 0,75 | 0,79 | 0,8 | 0,85 | 1,00 |
При увеличении числа наблюдений - n , СКО - (среднеквадратичное отклонение) случайной погрешности результата измерений S(X) уменьшается по закону обратной пропорциональности - 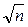 .
.
Этим руководствуются при выборе n для разумного уменьшения S(Х), например, по сравнению с НСП результата измерений Q, не зависящей от n (до выполнения условия Qi / S(Х) ³ 8 , дальнейшее увеличение n не имеет смысла). Как правило, выбор числа наблюдений производится при разработке МВИ.
Для обеспечения качества производства в цехахпредприятия должна быть правильно оформленная технология измерений. С июня 1997 года в Российской Федерации действует ГОСТ Р 8.563-96 «ГСИ. Методики выполнения измерений». Согласно этого стандарта, каждый параметр или размер должен быть оформлен по требованиям вышеуказанного стандарта под названием «Методика выполнения измерений» как новый стандарт и аттестован органами, аккредитованными институтамиГосстандарта Российской Федерации. В сфере производства различных предприятий содержится большое количество параметров, подлежащих измерениям и контролю, и если все измерения оформлять методиками выполнения измерений строго по вышеуказанному стандарту, то их количество будет загромождать перечислением их в технологическом процессе отдельными списками. На все ли параметры необходимо иметь документированную методику выполнения измерений строго по требованиям ГОСТ Р 8.563 – 96? В тексте самого ГОСТа есть фраза, которая, отвечая на этот вопрос, отмечает, что не все измерения должны иметь документированную МВИ, разработанную и утверждённую по вышеуказанному ГОСТу. Из формулы (9.15) рассмотрено соотношение, которое иллюстрирует однократность измерений и далее рассматривается в разделе 9.2 Прямые измерения с однократными наблюдениями. В журнале «Главный метролог» № 6 2013 года в статье В.А. Брюханова достаточно подробно рассматривается вопрос о противоречиях и дискуссиях относительно закона «Об обеспечении единства измерений», ГОСТ Р 8. 563-09 и термина точность измерений. В пункте 3.4 ГОСТ 8.563-09 есть текст о точности измерений. «Показатель точности измерений: установленная характеристика точности любого результата измерений, полученного при соблюдении требований и правил данной методики». Методики, читай МВИ по ГОСТу. А если МВИ не требуется как НД? Тогда как? Вопросы возникают сразу у любого студента или обучающегося, не имеющего производственного опыта технологических или лабораторных измерений. А в настоящее время такие вопросы могут возникнуть и у действующих молодых технологов и конструкторов на предприятиях. Что надо понимать под «характеристикой точности»? Какой смысл вкладывается в слово «установленная»? Кем, когда и на каком основании устанавливается «характеристика точности любого результата измерений»? Что же это такое «показатель точности измерений»? Любой метролог, имеющий большой стаж производственной и преподавательской деятельности, из своего опыта точно знает, что термин «точность измерений» имеет качественный оттенок, и он показывает насколько близок результат измерений к действительному значению измеряемой величины. В старом и отменённом ГОСТ 16263-70 давалось следующее определение этого термина: «Точность измерений – качество измерений, отражающее близость их результата к истинному значению измеряемой величины». В международном словаре в области метрологии есть аналогичное определение: «Точность измерений – степень близости результата измерений к истинному значению измеряемой величины». На страницах журнала «Советник метролога» В.А. Брюханов в своей статье призвал метрологов и заинтересованных в метрологии работников дать ответы на анкетный опрос по перечню показателей измерений. Читатели журнала выбрали варианты ответов на вопрос о том, какие же из них следует относить к показателям точности измерений. Вариантв ответов выглядели следующим образом:
А) погрешность измерений;
Б) границы, в которых погрешность измерений находится с заданной вероятностью;
В) среднее квадатическое отклонение погрешности;
Г) среднее квадратическое отклонение случайной составляющей погрешности измерений;
Д) сходимость результатов измерений;
Е) воспроизводимость результатов измерений;
Ж) среднее квадратическое отклонение систематической составляющей погрешности измерений;
З) границы, в которых неисключённая систематическая составляющая погрешности измерений находится с заданной вероятностью;
И) стандартная неопределённость измерений по типу А;
К) стандартная неопределённость измерений по типу Б;
Л) суммарная стандартная неопределённость измерений;
М) расширенная неопределённость измерений;
Н) прецизионность измерений.
Рссматривая все эти варианты и отбрасывая несоответствия, журнал «Главный метролог» № 6 за 2013 год в статье В.А. Брюханова даёт рекомендацию: Показатели точности измерений:
1 По концепции погрешности измерений:
1.1 Границы, в которых погрешность измерений находится с заданной вероятностью (интервальная характеристика);
1.2 Среднее квадратическое отклонение погрешности (точечная характеристика);
2 По концепции неопределённости измерений:
2.1 Расширенная неопределённость измерений для заданной вероятности (интервальная характеристика);
2.2 Суммарная стандартная неопределённость измерений (точечная характеристика).
Дата добавления: 2015-01-13; просмотров: 1452;
