Погрешности измерений. Погрешностью измерения называется отклонение результата измерения от истинного значения измеряемой физической величины

Погрешностью измерения называется отклонение результата измерения от истинного значения измеряемой физической величины. Так как истинное значение измеряемой величины неизвестно, то при количественной оценке погрешности пользуются действительным значением физической величины. Это значение находится экспериментальным путем и настолько близко к истинному значению, что для поставленной задачи может быть использовано вместо него.

По способу количественного выражения погрешности измерения делятся на абсолютные, относительные и приведенные. Абсолютной погрешностью Δ, выражаемой в единицах измеряемой величины, называется отклонение результата измерения Х от истинного значения Х_и , или Х_д , т. е Δ = =Х_изм. – Х_д;

По характеру (закономерности) изменения погрешности измерений подразделяются на систематические, случайные и грубые (промахи).

Установление числа наблюдений при измерениях: не следует приравнивать (отождествлять) понятие результат измерения с наблюдением при измерении. Наблюдение при измерении - экспериментальная операция, выполняемая в процессе измерений, в результате которой получают одно значение величины (отсчет) - результат наблюдения, подлежащее обработке для получения результата измерения. Поэтому результат измерения расчетная величина.

В процессе измерения, получая результаты наблюдений, у оператора всегда присутствуют два вида погрешностей, проявляющиеся одновременно в форме суммы: - Δ = Θ + S(х); или Δ = θ + σ; где первая составляющая суммы это систематическая погрешность, а вторая – случайная погрешность. Таким образом, при измерениях, показания СИ при любых наблюдениях можно представить как выражение из трех определений: X_изм. = X_д + Θ + S(х).

Остановимся сначала на систематических погрешностях, а случайную погрешность рассмотрим ниже, т.к. это связано со статистическими методами. Систематические погрешности Δ_с – составляющие погрешности измерений, остающиеся постоянными или закономерно изменяющиеся при многократных или повторных измерениях одной и той же физической величины в одних и тех же условиях.

Различают измерения с однократными и многократными наблюдениями. Наиболее распространены (в производстве) измерения с однократными наблюдениями. Это обусловлено обстоятельствами экспериментальной или производственной необходимости (разрушение объекта измерения в процессе наблюдения, невозможность повторения наблюдения, экономической целесообразностью и т.д.), а также, возможностью пренебречь случайными погрешностями, ситуациями, когда случайные погрешности доминируют, но доверительная граница погрешности результата измерения с однократным наблюдением не превышает допустимую погрешность измерений. Случайную погрешность считают пренебрежимо малой по сравнению с систематической (неисключенным остатком систематической погрешности - НСП) – старый термин. Термин по РМГ 29 – 99, НСП – неисключенная систематическая погрешность.

Граница НСП в практике пользования СИ часто трудно определима, тем более, когда надо определиться с тем понятием - однократное или многократное измерение необходимо произвести вот сейчас в данном, конкретном случае. В таких случаях два - три наблюдения при измерениях, имеющие различные значения и представляют причины для границ доверительной погрешности, в зависимости от предельных погрешностей метода измерения, который был Вами выбран, предельных погрешностей СИ, предельных погрешностей рабочих эталонов. Все эти составляющие систематических погрешностей входят в обозначение как N – число слагаемых и, согласно РМГ 29 – 99, определение НСП выполняется по формулам (7.1) и (7.2)

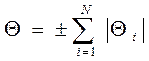, (7.1)

где Q_i - граница i – й составляющей неисключенной систематической погрешности при N £ 3;

N - число слагаемых, состоящих из пределов допускаемых основных и дополнительных погрешностей СИ, рабочих эталонов и т. д.

При N ³ 4 , расчет ведется по формуле (7.2)

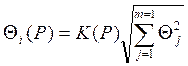, (7.2)

Для повышения надежности таких измерений, исключая промахи, делают два или три наблюдения, и за результат измерений принимают среднее арифметическое значение результатов этих наблюдений.

Измерения с числом наблюдений n ³ 4 относят, условно к измерениям с многократными наблюдениями и выполняют статистическую обработку ряда результатов наблюдений для получения информации о результате измерений и о случайной составляющей погрешности этого результата. Дальнейшее рассмотрение систематических погрешностей следует вести с учетом исключения их проявлений.

8 Учет систематической погрешности и способы их уменьшения

Систематические погрешности, как правило, не проявляются при выполнении наблюдений и вычислений результатов измерений, но способны существенно исказить результаты! При разработке выбора СИ и МВИ, т.е. еще до начала измерений систематические погрешности более или менее полно исключаются (например, введением аддитивных или мультипликативных поправок). Поэтому при выполнении наблюдений и оценке результатов измерений имеют дело с не исключенными остатками систематических погрешностей - НСП. Для обнаружения НСП рекомендуется: провести измерение другим, максимально отличным от использованного, методом и сравнить результаты. Резко изменить условия наблюдений. Использовать другие экземпляры СИ, сменить оператора замеров, изменить время суток наблюдений, когда выключено технологическое оборудование. Далее провести контрольное измерение в лаборатории другого предприятия, в другом городе, в метрологическом учреждении, в котором имеются более точные СИ и МВИ. Далее выполнить теоретическую (расчетную) оценку НСП с привлечением имеющихся априорных знаний об ОИ, более точных или других моделях ОИ, методе и СИ. Все это касалось метода непосредственных измерений - метода непосредственной оценки сравнения с мерой.

Запишите формулировку методов согласно РМГ 29 – 99:

а) метод непосредственной оценки – метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений;

б) метод сравнения с мерой – метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой;

в) метод противопоставления - метод сравнения с мерой, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливаются соотношение между этими величинами;

г) дифференциальный метод – метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами;

д) нулевой метод - метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля. Пример - Измерение электрического сопротивления мостом с полным его уравновешиванием;

е) метод замещения - метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины. Пример - Взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов (метод Борда);

Пусть Мх - измеряемая масса. L1 и L2 - длины плеч коромысла весов. Сначала измеряемую массу помещают на одну из чашек весов и уравновешивают весы, помещая на другую чашку весов некоторый груз массой Т (например, гирю). При этом Мх = Т L2/L1. Затем снимают массу Мх и на эту же чашку помещают гири такой суммарной массы М, чтобы весы вновь уравновесились. При этом М = Т L2/L1. Из сопоставления этих выражений следует, что Мх = М при любом отношении L2/L1, причем не нужно знать значение Т;

ж) метод совпадений - метод сравнения с мерой, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадения отметок шкал или периодических сигналов. Например, измерение длины с помощью штангенциркуля с нониусом основано на использовании метода совпадений, наблюдают совпадение отметок на шкалах штангенциркуля и нониуса, при измерении частоты вращения стробоскопом - наблюдают совпадения положения какой-либо марки на вращающемся объекте в моменты вспышек известной частоты. Среди перечисленных методов существует метод компенсации погрешности по знаку - предусматривающий измерение с двумя наблюдениями, выполняемыми так, чтобы НСП входила в результат каждого из них с разными знаками. Пример - измеряется ЭДС с помощью потенциометра постоянного тока, имеющего паразитную термоЭДС. Проведя два наблюдения при противоположном направлении рабочего тока в потенциометре и взяв среднее значение, получим результат, свободный от этой погрешности. Еще пример - для исключения НСП из-за вариации, гистерезиса, мертвого хода верньерных механизмов, измерения проводят при подходе к определяемому отсчету слева и справа. Результат измерения вычисляют по формуле (8.1)

Х = (Х_сл + Х_спр) / 2 (8.1)

Кроме этого - метод рандомизации (перевод систематической погрешности в случайную) заключается в такой организации измерений, при которой фактор, вызывающий НСП, при каждом наблюдении действует по разному. Например:

а) для исключения влияния магнитного поля Земли наблюдения повторяют несколько раз, поворачивая ОИ каждый раз на некоторый угол, (обычно одинаковый) относительно силовых линий поля. За результат измерений принимают среднее арифметическое из всех наблюдений;

б) метод симметричных наблюдений применяется для устранения прогрессирующих систематических погрешностей, линейно меняющихся пропорционально времени;

в) используют следующее свойство любых двух наблюдений, симметричных относительно средней точки интервала наблюдений - среднее значение линейно прогрессирующей погрешности результатов любой пары симметричных наблюдений равно погрешности, соответствующей средней точке интервала;

г) ряд наблюдений выполняют через равные промежутки времени и вычисляют среднее арифметическое значение результатов симметрично расположенных наблюдений (симметрично относительно среднего по времени наблюдения). Как было сказано, они должны быть равны. Это дает возможность контролировать в ходе измерения, соблюдается ли условие линейности возрастания систематической погрешности.

Все приведенные методы (приемы), а также методы опосредованного сравнения с мерой должны учитываться при разработках МВИ.

После применения процедуры исключения систематических погрешностей в результат измерения вводятся поправки, или одна поправка, после чего измерения называются исправленными. После определения количества составляющих остатка систематических погрешностей делается расчет НСП. Неисключенные систематические погрешности отдельных наблюдений при измерениях включают в себя значение меры, используемой при поверке или калибровке СИ и искомой сумме составляющих систематической погрешности, следовательно, среднее значение измеряемой величины при N наблюдениях можно вычислить по формуле 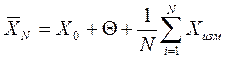(8.2)

, (8.2)

где первый член суммы – погрешность меры;

второй – систематическая погрешность;

третий – показание СИ и случайная погрешность.

Для описания случайной погрешности, необходимо вспомнить «дифференциальную функцию распределения», математическое ожидание, дисперсию и среднеквадратическое отклонение, которые изучались в курсе теоретической метрологии.