Косвенные измерения при нелинейной зависимости
При некоррелированных погрешностях измерений аi используется метод линеаризации путем разложения функции ¦(a1 ,......, am) в ряд Тейлора по формуле (9.21) /5/
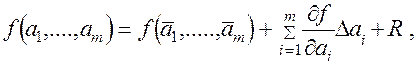 (9.21)
(9.21)
где D аi = аi - `аi - отклонение отдельного результата наблюдения аi от `аi;
R - остаточный член.
Метод линеаризации допустим, если приращение функции ¦ можно заменить ее полным дифференциалом. Остаточным членом  , пренебрегают, если
, пренебрегают, если 
где S (ai) - оценка СКО случайных погрешностей результата измерения аi .
При этом отклонения Dаi должны быть взяты из возможных значений погрешностей и такими, чтобы они максимизировали R.
Результат измерения `А вычисляют по формуле (9.22) /5/
А = f (`a1 ,.....,`ai), (9.22)
Оценку СКО случайной составляющей погрешности результата такого косвенного измерения S (A) вычисляют по формуле (9.23) /5/
 (9.23)
(9.23)
а e(Р) - по формуле (9.19).
Значение n эф, границы НСП Q(Р) и погрешность D (Р) результата косвенного измерения при нелинейной зависимости вычисляют так же, как и при линейной зависимости, но с заменой коэффициентов b на ∂ f / ∂ ai .
Метод приведения (для косвенных измерений с нелинейной зависимостью) применяется при неизвестных распределениях погрешностей измерений аi и при корреляции между погрешностями аi для получения результата косвенного измерения и определения его погрешности. При этом предполагается наличие ряда n результатов наблюдений аij измеряемых аргументов аi. Сочетания аij , полученных в j - м эксперименте подставляют в формулу (9.14) и вычисляют ряд значений Аi измеряемой величины А. Результат измерения А вычисляют по формуле (9.24) /5/
 (9.24)
(9.24)
Оценку СКО S (A) - случайной составляющей погрешности А вычисляют по формуле (9.25) /5/
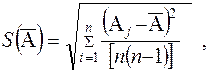 (9.25)
(9.25)
e(Р) вычисляют по формуле (9.14).
Границы НСП Q(Р) и погрешность D(Р) результата измерения А определяют описанными выше способами для нелинейной зависимости.
Дата добавления: 2015-01-13; просмотров: 1015;
