Средства измерений и их классификация по ГСИ

Классификация СИ по определяющим признакам.

В метрологии СИ принято классифицировать по виду, принципу действия и метрологическому назначению.

Различают следующие виды СИ:

- меры;

- измерительные устройства;

- измерительные установки;

- измерительные системы.

Мера – средство измерений, предназначенное для воспроизведения физической величины заданного размера.

Измерительное устройство – применяется самостоятельно или в составе измерительных установок и измерительных систем. В зависимости от формы представления сигнала измерительной информации измерительные устройства подразделяются на измерительные приборы и измерительные преобразователи.

Измерительный прибор – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия оператора.

Измерительный преобразователь – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и (или) хранения, но непосредственно не воспринимается оператором.

Измерительный прибор и измерительный преобразователь в блок– схеме соответственно подразделяются на четыре подтипа: два первых из них одинаковы, а два других имеют между собой различия.

Измерительная установка – совокупность функционально объединенных СИ (мер, измерительных приборов, измерительных преобразователей) и вспомогательных устройств, предназначенных для выработки сигналов измерительной информации в форме, удобной для непосредственного восприятия наблюдателем, и расположенных в одном месте. Обобщенная структурная схема СИ представлена на рисунке 10.1.

Для удобства анализа различных соединений СИ в Измерительные устройства или Информационно-Измерительные Системы между собой и со средствами автоматического управления любое устройство измерения принято рассматривать как некоторый преобразователь, служащий для преобразования входного сигнала Х в выходной сигнал Y. Такое представление Измерительных Устройств позволяет применять при анализе систем хорошо разработанный аппарат теории автоматического регулирования. Если входной и выходной сигналы представляют собой некоторые физические процессы, характеризуемые несколькими параметрами, то среди них различают информативные и неинформативные. Для конструкторов СИ и приборостроителей чрезвычайно важной является информация о внутренней структуре измерительного устройства. А они состоят из некоторого числа элементов (составных частей), предназначенных для выполнения определенных функций, таких, как:

- преобразование поступающего сигнала по форме или виду энергии;

- успокоение колебаний, защита от помехонесущих полей;

- коммутация электрических цепей, представление информации (цифровая, диаграммная по кругу или в ленту, только показывающая результат без регистрации и т.д.).

К элементам измерительных устройств относятся опоры, направляющие пружины, магниты, контакты, множительно-передаточные механизмы и т. д.

Основные элементы структурных схем СИ: меры, компараторы, первичные и вторичные преобразователи, устройства обработки информации, устройства представления и регистрации информации, каналы связи, вспомогательные элементы СИ.

Преобразовательный элемент - элемент СИ, в котором происходит одно из ряда последовательных преобразований измерительных величин.

Измерительная цепь - совокупность преобразовательных элементов СИ, обеспечивающая осуществление всех преобразований сигнала измерительной информации. Чувствительный элемент - первый в измерительной цепи преобразовательный элемент, находящийся под непосредственным воздействием измеряемой величины.

Измерительный механизм - часть конструкции СИ, состоящая из элементов, взаимодействие которых вызывает их взаимное перемещение.

Отсчетное устройство - часть конструкции СИ, предназначенная для отсчитывания значений измеряемой величины. Отсчётное устройство со шкалой и стрелкой может быть со шкалой равномерной, что косвенно свидетельствует о линейной или близко к линейной зависимости преобразовательного элемента. При необходимости более точного отсчёта к конструкции стрелки делают устройство зеркальной полосы так, чтобы, глядя на стрелку сверху вниз на шкалу, можно было бы совместить видимость тела стрелки с её тенью или отражением в зеркальной полосе, это делает отсчёт стого перпендикулярным к плоскости шкалы и исключает перекос или параллакс отсчёта. При неравномерности шкалы, т.е. при нелинейности преобразовательного элемента, необходимо стремиться к отсчётам в той части шкалы, которая по своим штриховым отметкам наиболее приближалась к равномерной части шкалы. Вот почему для таких приборов существует рекомендация измерения проводить в последней трети шкалы. Для современных электронных приборов характерна не шкала, а табло или дисплей цифровой информации. Такое отсчётное устройство имеет ряд преимуществ, а также ряд недостатков. Преимущество таких отсчётных устройств заключается в преобладающей точности показаний результата наблюдений, особенно в приборах с плавающей запятой. При показаниях таких приборов на дисплее часто видно как в последнем разряде после запятой цифра мигает или зажигается неустойчивыми, бегающими цифрами (допустим – семь, восемь, шесть и опять семь). Этот признак удобен тем, что можно судить о степени предельно допустимой погрешности применяемого вами прибора, даже не имея точной информации о его поверке. Недостаток таких приборов заключается в том, что в ходе измерения не видно всей шкаля и диапазона измерений и необходимо обращаться к дополнительной информации о его пределах измерений.

Рисунок 10.1 – Обобщенная структурная схема СИ

Структурная схема измерительного устройства прямого действия представлена на рисунке 10.2

а)

б)

Рисунок 10.2 - Структурная схема измерительного устройства действием сравнения

Ниже будет приведены структурные схемы измерительных устройств прямого и уравновешивающего действий, но без измерительного механизма и отсчетного устройства, а только сигнального порядка для восприятия электронных средств контроля и управления УВК - управляющим вычислительным комплексом. Однако на выходе в конечном преобразовательном элементе, формирующем выходной сигнал (усиление по мощности, преобразование по частоте колебаний и т.д.) таким образом, что его можно регистрировать, передавать на расстояние, хранить и обрабатывать в статистическую информацию.

а)

б)

Рисунок 10.3 – Структурная схема измерительного устройства прямого и уравновешивающего действий без измерительного механизма

Следующим элементом, который необходимо подробнее раскрыть, является отсчетное и регистрирующее устройства, где основным узлом является узел показания результата. Показанием называют значение величины, определяемое по отсчетному устройству и выраженное в единицах этой величины или отградуированное в шкале этих величин. Отсчетное устройство представляет собой цифровое табло или, в подавляющем большинстве случаев, шкалу с указателем.

Для шкальных, отсчетных устройств принято использовать ряд понятий, сущность большинства из которых легко установить по рисунку 10.4.

Статические характеристики и параметры измерительных устройств.

В общем случае, когда при измерениях все условия измерения, а также входные и выходные сигналы и наблюдения не изменяются как функция от времени, остаются параметрами постоянными, то такие измерения называют статическими (стационарными или равновесными).

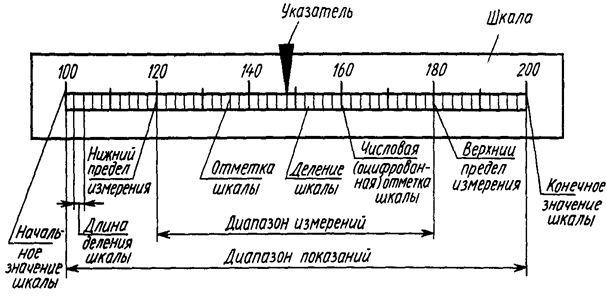
Рисунок 10.4 - Схема отсчетного устройства измерительного прибора

Статической характеристикой измерительного устройства называют функциональную зависимость выходного сигнала от входного в статическом режиме работы этого устройства.

Статическая характеристика описывается как некоторое нелинейное уравнение (10.1) (уравнение преобразования) /8/

Y=f (X), (10.1)

Для измерительных преобразователей, а также измерительных приборов с неименованной шкалой или со шкалой, отградуированной в единицах, отличных от единиц измеряемой величины статическую характеристику принято называть функцией преобразования. Для измерительных приборов иногда статическую характеристику называют характеристикой шкалы. Определение статической характеристики связано с выполнением градуировки, поэтому для всех средств измерений используют понятие градуировочной характеристики, под которым понимают зависимость между значениями величин на выходе и входе СИ, составленную в виде таблицы, графика или формулы.

На рисунке 10.5 показаны статические характеристики измерительных устройств.

За исключением специальных случаев, основное требование, предъявляемое к статической характеристике измерительных устройств, сводится к получению линейной зависимости между выходной величиной и входной величиной. На практике это требование реализуется в общем случае только с некоторой принятой заранее погрешностью.

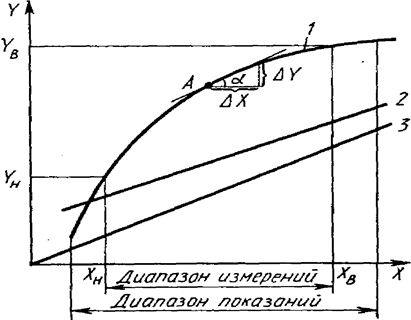
Рисунок 10.5 - Статическая характеристика измерительного устройства

Кроме статической характеристики для определения метрологических свойств измерительных устройств используется ряд параметров.

На рисунке 10.5 показаны статические характеристики 1, 2, 3 графически, где также графически указаны ранее упомянутые понятия - диапазоны показаний и диапазона измерений – (Хн, Yн) - нижние пределы и – (Хв, Yв) - верхние пределы.

Диапазон показаний - область значения шкалы, ограниченная конечным и начальным значением шкалы.

Диапазон измерений (рабочая часть шкалы) - область значений измеряемой величины (на шкале прибора), для которой нормированы допускаемые погрешности СИ - о чем Вы уже знаете из раздела о погрешностях!

В частном случае, когда Вы используете всю шкалу для измерений, указанные диапазоны могут совпадать.

Часто диапазон измерений называют рабочим диапазоном преобразований.

Верхний предел измерения - наибольшим значением диапазона измерений.

Нижний предел измерения - наименьшим значением диапазона измерений.

Из изложенного соотношения вытекает, что диапазон измерений определяется разностью значений верхнего и нижнего пределов измерений (Хв - Хн;) и (Yв - Yн). Для количественной оценки влияния на выходной сигнал измерительного устройства входного сигнала в произвольной точке А статической характеристики служит предел отношения приращения dY выходного сигнала к приращению dX входного сигнала, когда последнее стремится к нулю, т.е. производная в выбранной точке. Наглядно это видно из формулы (10.2) /8/

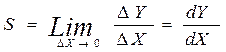, (10.2)

Применительно к измерительным приборам этот параметр называют - чувствительностью и определяют как отношение значения сигнала на выходе измерительного прибора к вызывающему его изменению измеряемой величины. Графически она определяется тангенсом угла наклона tg α касательной к кривой характеристики, проведенной в выбранной точке А статической характеристики.

Если статическая характеристика измерительного прибора нелинейна (кривая 1 на рисунке 10.5), то его чувствительность будет различной в разных точках на кривой, а шкала прибора - неравномерной. Приборы с линейной характеристикой имеют шкалу равномерную в любой точке и также неизменную чувствительность - (прямые 2 или пропорциональная 3 на рисунке 10.5).

У измерительных преобразователей статистические характеристики, как правило, являются линейными (смотри формулу (10.3) /8/)

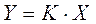, (10.3)

где К - коэффициент преобразования (или при использовании преобразователя в системах автоматического регулирования - коэффициент передачи), определяемый как отношение сигнала на выходе измерительного преобразователя, отражающего измеряемую величину, к вызывающему его сигналу на входе преобразователя.

Для измерительного прибора важным параметром является цена деления, определяемая как разность значений величин, соответствующих двум соседним отметкам шкалы.

Физически цена деления определяется количеством единиц входной величины, содержащихся в одном делении шкалы измерительного прибора.

Цена деления конечно связана с числом делений n шкалы измерительного прибора. Последнее в свою очередь связано с погрешностью измерительного прибора, обычно представляемой его классом точности Λ. Число делений шкалы измерительного прибора, как правило, в первом приближении определяется из соотношения показанного в формуле (10.4) /8/

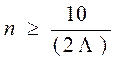, (10.4)

При выполнении условия (10.4) число делений шкалы выбирают таким, чтобы цена деления составляла целое число единиц измеряемой величины.

В НД и в научно-технической литературе используется понятие порога чувствительности (порога реагирования) измерительного устройства, под которым понимают то наименьшее изменение входного сигнала, которое вызывает уверенно фиксируемое изменение выходного сигнала. Как правило, оператор, наблюдатель, осуществляющий измерение или контроль параметров, уверенно может заметить смещение стрелки на половину деления шкалы, поэтому порог чувствительности можно считать равным половине цены деления, а если учесть при этом соотношение (10.4), то в первом приближении порог чувствительности равен классу точности Λ. Одним из важных условий получения корректных результатов измерений является учет взаимодействия измерительных устройств между собой и с объектом измерений. При подключении измерительного устройства или преобразователя к объекту измерений он потребляет некоторую энергию или мощность от объекта. Аналогичная ситуация имеет место при подключении измерительного прибора или преобразователя к выходу предыдущего по цепи измерения преобразователя. Это определяет необходимость учитывать свойства измерительных устройств отбирать или отдавать энергию через свои входные или выходные цепи. И тогда, хотим мы этого или не хотим, электрические цепи прибора подчиняются законам электротехники. Поэтому, в качестве характеристики указанного свойства, принято использовать для измерительных устройств понятие – входного импеданса (полного или кажущегося сопротивления), а для измерительных преобразователей понятия входного и выходного импедансов. В общем случае под импедансом Z понимают отношение обобщенной силы N к обусловленной ею обобщенной скорости W. Импеданс вычисляется по формуле (10.5) /8/

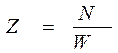, (10.5)

В настоящее время понятие входного и выходного импедансов широко используется для электрических измерительных устройств, а так как применение вычислительных комплексов и управляемых вычислительных машин или также комплексов (УВМ, УВК) являются электронными средствами, то все более и более сфера электрических СИ в нашей жизни расширяется. При этом импеданс определяется как отношение напряжения к току (закон Ома). Применительно к измерительным устройствам для неэлектрических величин в каждом отдельном случае требуется проведение исследований для установления наиболее целесообразной формы представления входного и выходного импедансов и их соответствия масштабу измеряемых величин.

Динамические характеристики измеряемых устройств, режим работы измерительного устройства, при котором значения выходного и входного сигналов изменяются во времени, называют динамическими (нестационарными или неравновесными).

Практически все измерительного устройства имеют в своем составе инерционные элементы, а именно: подвижные механические узлы, электрические и пневматические емкости, индуктивности, элементы, обладающие тепловой инерцией и т.д. Наличие инерционных элементов определяет инерционность всего измерительного устройства. Это приводит к тому, что в динамическом режиме мгновенное значение выходного сигнала измерительного устройства зависит не только от мгновенного значения входного сигнала, но и от любых изменений этого сигнала, т.е. от его первой и второй производных и производных более высокого порядка. Указанные инерционные свойства измерительных устройств определяются динамической характеристикой.

Динамическая характеристика измерительного устройства в общем случае это зависимость между информационными параметрами выходного и входного сигналов и временем или зависимость выходного сигнала от входного в динамическом режиме.

Динамическую характеристику измерительного устройства принято описывать дифференциальным уравнением, передаточной или комплексной частотной функциями.

В подавляющем большинстве случаев динамическая характеристика измерительных устройств в линейной части статической характеристики (для измерительных устройств с линейной статической характеристикой во всем диапазоне преобразований) может быть описана дифференциальным уравнением (10.6) /8/

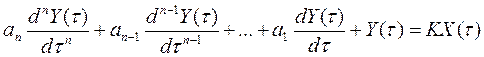, (10.6)

или соответствующей передаточной функцией(10.7) или (10.8) /8/

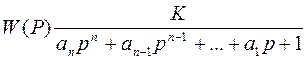, (10.7)

либо

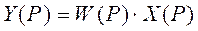, (10.8)

где Y(p) и X(p) - выходной и входной сигналы измерительного устройства как функции времени;

n - число, определяющее порядок производной.

Передаточную функцию W(p) из формулы (10.7) можно рассматривать как коэффициент преобразования измерительного устройства в динамическом режиме. Передаточная функция, как и дифференциальное уравнение, является исчерпывающей характеристикой инерционных свойств измерительного устройства. Она позволяет определять реакцию измерительного устройства на входные сигналы, изменяющиеся во времени по любому закону. Передаточную функцию измерительных устройств удобно использовать при анализе работы последних в автоматических системах регулирования. Ее определяют обычно через переходную или временную характеристику, которая определяется как изменение во времени выходного сигнала h (t) измерительного устройства при подаче на его вход скачкообразного сигнала, равного по значению единице входной величины.

Если высота скачкообразного входного сигнала не равна единице, а имеет некоторое значение Х_А, то по переходной характеристике можно определить выходной сигнал, используя выражение (10.9) /8/

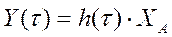, (10.9)

Для определения инерционных свойств измерительных устройств по переходным характеристикам обычно используют заимствованное из теории автоматического регулирования понятие динамического звена. Переходные характеристики и передаточные функции типовых динамических звеньев известны, что позволяют по форме переходной характеристики измерительного устройства отождествить его с каким-либо типовым динамическим звеном, а, следовательно, определить форму передаточной функции используемого измерительного устройства. Описанную процедуру принято называть идентификацией.

На нижеприведенном рисунке 10.6 показаны типичные для измерительных устройств формы переходных процессов, или кривые разгона.

Для получения этих процессов, в нулевой (для простоты) момент времени, входной сигнал измерительного устройства скачком изменяется на величину Х_а от некоторого значения Х₁ до Х₂, как на рисунке 10.6 а. По окончании переходного процесса выходной сигнал измерительного устройства изменяется на величину Y_а от значения Y₁ до Y₂. Для определения коэффициента преобразования К измерительного устройства достаточно вычислить отношение Y_a/X_a. Переходные процессы, показанные на рисунке 10.6 б, 10.6 в, 10.6 г, соответствуют типовым усилительному (безнерционному), апереодическому первого порядка и колебательному звеньям /8/.

Процесс, представленный на рисунке 10.6 б, характерен для электронных измерительных устройств, а процессы, представленные на рисунке 10.6 в и 10.6 г - для большого числа измерительных устройств, основанных на прямом преобразовании. Кривая на рисунке 10.6 в представляет собой экспоненту, а величина Т (подкасательная) называется постоянной времени. Она определяет собой время, за которое выходной сигнал достиг бы нового установившегося значения, если бы изменялся с постоянной скоростью, равной скорости в момент скачкообразного изменения входного сигнала.

Постоянная времени используется для характеристики динамических свойств измерительных устройств. Проведение касательной и кривой переходного процесса сопряжено с погрешностями, поэтому значения постоянной времени определяют как интервал времени, за который выходной сигнал изменяется на 0,632 от своего приращения Ya на рисунке 10.6 в. Корректность такого определения легко доказывается математически, но мы этого сейчас делать не будем, так как курс лекций очень сокращен. Колебательное динамическое звено, а следовательно, и измерительное устройство, в котором имеет место переходный процесс, показанный на рисунке 10.6 г, можно рассматривать как соединение двух апериодических звеньев с постоянными времени Т₁ и Т₂. При этом в зависимости от соотношений Т₁иТ₂, переходный процесс будет различен. Если (Т₁/Т₂) < 2, то он имеет форму кривых 1 и 2, а при (Т₁/Т₂) > 2 - форму кривой 3 на рисунке 10.6 г. Переходные процессы, показанные на рисунках 10.6 д и 10.6 е, характерны для случаев, когда дифференциальное уравнение, описывающее динамику измерительного устройства, имеет порядок более чем второй. В этих случаях принято рассматривать измерительное устройство как совокупность нескольких, соединенных последовательно типовых динамических звеньев. Например, измерительное устройство с переходным процессом, показанным на рисунке 10.6 д, можно рассматривать как соединение звена чистого запаздывания со временем запаздывания tз и апериодического звена с постоянной времени Т (для графического определения значений tз и Т достаточно провести касательную к точке А на рисунке 10.6 д. Измерительное устройство с переходным процессом, показанным на рисунке 10.6 е, можно рассматривать как соединение звена чистого запаздывания и колебательного звена. Для всех измерительных устройств важным является время установления выходного сигнала (или показаний) Т_п на рисунке 10.6, которое также называют временем реакции. Оно определяет собой отрезок времени, необходимый для завершения переходного процесса при скачкообразном изменении входного сигнала. Все рассмотренные переходные процессы на рисунке 10.6 теоретически заканчиваются только при бесконечном значении времени. Поэтому, за время реакции Тп обычно принимают время, за которое выходной сигнал измерительного устройства, приближаясь к новому установившемуся значению, входит в некоторую зону, отличающуюся от этого значения на (плюс, минус) 5 % от изменения выходного сигнала, соответствующего данному скачкообразному входному сигналу. Значение времени реакции может быть приближено определено через постоянную времени измерительного устройства из соотношения (10.10) /8/

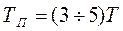, (10.10)

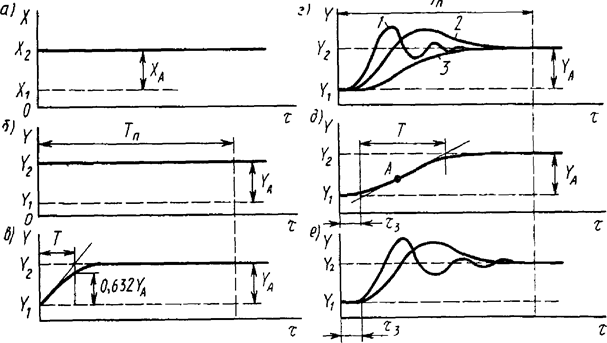
Рисунок 10.6 - Типичные формы переходных процессов для измерительных устройств

Дифференциальные уравнения и передаточные функции рассмотренных наиболее типичных по инерционным свойствам измерительных устройств приведены в таблицу 10.1.

Таблица 10.1 – Дифференциальные уравнения и передаточные функции, наиболее типичные по инерционным свойствам измерительных устройств

Кривая переход процесса	Дифференциальное уравнение	Передаточная функция
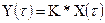
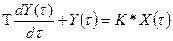
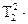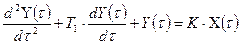
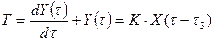
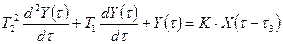
Рисунок 10.6 б   Рисунок 10.6 в     Рисунок 10.6 г     Рисунок 10.6 д   Рисунок 10.6 е		К

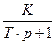
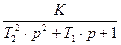
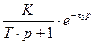
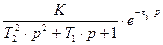
Мы уже знакомы с методами измерений, но с применением измерительных устройств этот раздел имеет небольшое отличие и в то же время схожесть. Еще раз кратко их перечисляю:

- метод непосредственной оценки;

- метод сравнения с мерой;

- дифференциальный метод;

- нулевой метод;

- метод замещения;

- метод совпадения (или метод «нониуса») при его схожести, отметим его отличительность: В данном случае применяются две меры с разными ценами деления, которые отличаются на размер оцениваемого разряда отсчетов, но при условии, что в приборе применяется две шкалы - одна неподвижная - отсчетная и другая - подвижная - показывающая, но чем - то схожая со шкалами штангенциркуля!

Пусть имеем одну калиброванную меру с ценой деления DХ₁ и изменяемую величину DХ, которая меньше цены деления. В этом случае используется вторая мера с ценой деления DХ₂. Таким образом, если чувствительность необходимо увеличить в «n» раз, то соотношение между ними будет иметь вид формулы (10.11) /11/

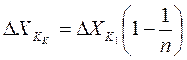, (10.11)

В частности, при n = 10 соотношение имеет вид формулы (10.12) /11/

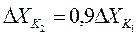(10.12)

Для того чтобы были понятны формулы, приведем рисунок 10.7, на котором изображены эти шкалы

Рисунок 10.7 - «Нониусный» метод измерения

Измеряемую величину DХ устанавливают между нулевыми отметками мер и находят число Nх, равное номеру совпавших рисок деления мер, как на рисунке. В этом случае справедливо соотношение:

,

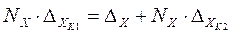откуда:

,

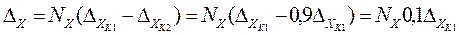Метод «нониуса» находит широкое применение при измерении временных интервалов двух близких частот (биений) и в других случаях.

В настоящее время существует еще и классификация методов измерительных преобразований, основанная на концепции измерительных преобразований. Любой измерительный процесс представляет собой последовательное преобразование сигнала измеряемой величины в величину, ради которой была поставлена задача измерения. В связи с этим любое СИ представляется как последовательно соединенные звенья, передающие сигнал измерительной информации от входа к выходу и образующие как бы канал преобразования. Тогда, в общем случае, любой метод измерения можно представить как последовательное преобразование измеряемой информации в вид, удобный для восприятия наблюдателем. В зависимости от состава результирующей погрешности и погрешности отдельных преобразователей различают методы прямого и уравновешивающего преобразований.

При методе прямого преобразования входной параметр последовательно проходит все преобразователи разомкнутой цепи преобразования и по выходному отсчетному устройству оценивается результат измерения (здесь движение информации происходит только в одну сторону). Погрешность такого средства измерения полностью определяется погрешностью всех преобразователей цепи преобразования. При методе уравновешивающего преобразования в измерительных устройствах существует, как минимум, два канала преобразования: прямой и обратный. Выход канала прямого преобразования (КПП) подается на вход отсчетного устройства и одновременно на вход канала обратного преобразования (КОП), предназначенного для преобразования выходного сигнала КПП в величину, аналогичную по физической природе входной величине; на вход КПП подается разность между измеряемой величиной и выходным сигналом КОП. Результирующая погрешность такой структуры практически полностью определяется погрешностью КОП (влияние КПП ничтожно мало при соответствующем выборе коэффициента его преобразования). Метод прямого преобразования аналогичен методу непосредственной оценки, а метод уравновешивающего преобразования - нулевому методу и, иногда, методу совпадения с нулевым одновременно при общепринятой классификации методов измерений /11/.