Экспериментальная установка и методика измерений

Метод определения коэффициента вязкости в данной работе основан на использовании формулы Пуазейля (18.8) для объёмного расхода 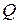при ламинарном протекании жидкости через трубу. Из нее и (18.7) выразим :

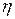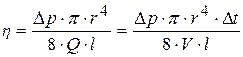, (18.10)

где 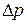– разность давлений на концах капилляра; 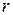– радиус капилляра; 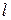– длина капилляра; 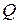– расход жидкости объемом 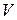за время .

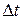Установка (рис. 18.3) состоит из герметичного сосуда 1, разделенного на две равные половины пробкой 2. В нижней половине сосуда расположен измерительный капилляр 3, конец которого выходит через пробку в верхнюю часть. В верхней половине сосуда находится более толстая (по сравнению с капилляром) трубка 4 (воздуховод), также соединяющая через пробку нижнюю и верхнюю части сосуда. Исследуемая жидкость 5 в процессе измерения перетекает через капилляр 3 из верхней части сосуда в нижнюю. Воздух при этом через воздуховод переходит из нижней части в верхнюю. Уровни жидкости в верхней и нижней половинах сосуда измеряются по шкале 6, имеющей нуль в средней части.

Обратное перемещение жидкости (для проведения повторного измерения) осуществляется поворотом сосуда на 180° на горизонтальной оси 7, вращающейся во втулке 8. Для предотвращения произвольного переворачивания сосуда ось имеет прямоугольное основание 9, которое перемещением оси вдоль втулки вводится в прямоугольный паз втулки.

Разность давлений 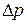на концах капилляра 3 создается за счет разности 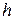между уровнями жидкости в верхней и нижней половинах сосуда (рис.18.4). Это – гидростатическое давление, оно равно:

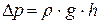. (18.11)

Высота 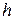определяется суммой высот столбов в верхней 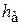и нижней 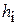частях сосуда. Так как установка выполнена симметрично относительно центра, то 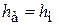, и

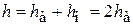. (18.12)

Таким образом, из (18.12) видно, что разность давлений на концах капилляра определяется уровнем жидкости и будет меняться. В то же время формула Пуазейля требует постоянного давления. Поэтому необходимо брать возможно меньший объем вытекающей жидкости 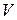и для расчетов брать среднее значение между начальным и конечным уровнями в каждом опыте. Например, для верхнего уровня 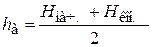; и

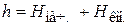. (18.13)

Чем меньший объем взят для вычисления результата, тем точнее будет формула Пуазейля. Однако при этом возникает погрешность измерения 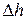, т.е. разности начального и конечного уровней при истечении объёма :

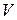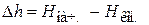. (18.14)

Оптимальным для данной установки будет разность уровней .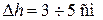

Если – внутренний радиус сосуда (см.рис.18.4), то

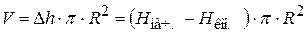, (18.15)

так как объем 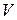вытекающей жидкости равен произведению изменения уровня 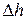жидкости в сосуде на площадь поперечного сечения сосуда .

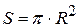Таким образом, расчетная формула приобретет вид:

;

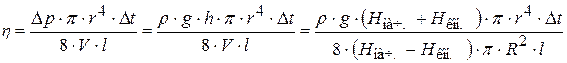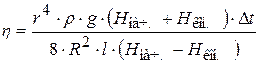(18.16)

В начальную часть формулы (18.16) входят постоянные величины, их следует вычислить и объединить в одну постоянную (для данной установки) величину :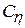

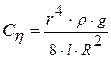. (18.17)

Переменные величины также объединим:

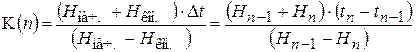, (18.18)

где n – номер опыта. Тогда

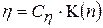. (18.19)