Экспериментальная часть. Приборы и оборудование: стеклянный сосуд с краном, пробка с капилляром, штатив, секундомер, мерный стакан (колба)

Приборы и оборудование: стеклянный сосуд с краном, пробка с капилляром, штатив, секундомер, мерный стакан (колба), линейка, вода.

В предлагаемом методе определения динамического коэффициента вязкости используется истечение воздуха через капилляр. Известно, что скорости истечения бесконечно тонких цилиндрических слоев воздуха, расположенных на различных расстояниях от оси капилляра, различны и распределены по сечению капилляра по параболическому закону. Наибольшая скорость будет на осевой линии капилляра и, по мере приближения к стенкам, скорость уменьшается, а слой, прилегающий к стенке, неподвижен, т.е. "прилипает" к ней.

Между слоями, движущимися с различными скоростями, возникает сила внутреннего трения (сила вязкости). При установившемся движении сила вязкости, действующая на элементарный объем и приложенная к боковой поверхности цилиндра, уравновешивает разность сил давлений, действующих на основание цилиндра. На концах капилляра при протекании по нему воздуха возникает разность давлений 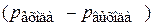. При установившемся движении воздуха она будет неизменной. При малых скоростях течения объем воздуха, протекающего через сечение капилляра, равен:

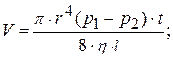
отсюда

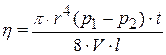. (19.1)

где 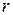– радиус капилляра; 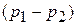– разность давлений в начале и конце капилляра; 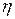– динамический коэффициент вязкости; 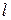– длина капилляра; 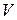– объем газа, протекшего через сечение капилляра за время .

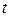Таким образом, для определения коэффициента вязкости достаточно измерить разность давлений, время истечения газа, его объем, радиус и длину капилляра.

Схема установки представлена на рис. 19.1. Установка состоит из стеклянного сосуда А со шкалой C. Верхняя часть сосуда закрыта пробкой с капилляром B, а в нижней имеется трубка с краном К. Перед началом работы кран закрыт, сосуд заполнен водой на 3/4 объема и плотно закрыт пробкой с капилляром. Если открыть кран К, то вода из сосуда А будет вытекать каплями. 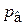При этом объем воды, вытекающий из сосуда, равен объему воздуха, прошедшего через капилляр , а давление у открытого конца трубки D равно сумме давлений: давления воздуха, находящегося над поверхностью воды в сосуде А, и гидростатического давления :

.

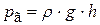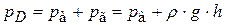Это давление уравновешивается атмосферным:

.

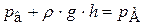Учитывая, что давление у верхнего конца капилляра равно атмосферному, разность давлений на концах капилляра выразится:

.

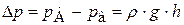Поскольку в процессе опыта давление столба воды уменьшается (за счет истечения), то берут среднее значение

,

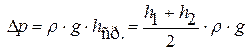и выражение для коэффициента динамической вязкости примет вид:

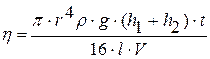. (19.2)