Теоретическое введение. Теплота , приданная системе (телу), расходуется на изменение ее внутренней энергии и на совершение работы .

Теплота 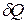, приданная системе (телу), расходуется на изменение ее внутренней энергии 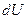и на совершение работы .

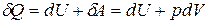(20.1)

Уравнение (20.1) – первое начало термодинамики. Символ 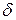(в некоторых учебниках используется обозначение 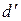) указывает на то, что бесконечно малые изменения 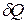и не являются полными дифференциалами, то есть количество теплоты 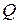и работа 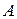зависят от пути процесса, по которому изменяется состояние системы. Только внутренняя энергия 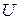является функцией состояния системы и от пути процесса не зависит.

При поглощении веществом теплоты 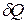его температура, как правило, увеличивается. Отношение 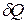к повышению температуры 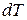называется теплоемкостью вещества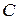

(20.2)

Так как величина 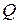зависит от характера процесса, то и теплоемкость 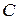от пути процесса зависит. Поэтому при определении теплоемкости необходимо указывать, каким именно способом изменяется температура. Часто встречающиеся виды процессов – при постоянном объеме ( ) – изохорический и при постоянном давлении ( ) – изобарический. Соответствующие им теплоемкости обозначают и .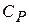

Для газов эти величины связаны друг с другом простым образом. По определению

, . (20.3)

Из (20.1) 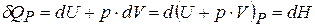, 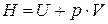– энтальпия, или теплосодержание.

При постоянном объёме 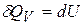, так как работа .

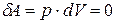Отсюда следует, что теплоемкост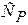и и 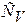есть частные производные от энтальпии и внутренней энергии по температуре (при постоянных давлении и объеме соответственно). Уравнения

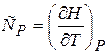и 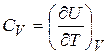(20.4)

можно рассматривать как определения. Они позволяют найти и 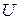термодинамической системы, если известны зависимост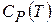и или .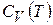

Каждое состояние термодинамической системы характеризуется совокупностью значений физических величин, отражающих ее свойства. Величины, имеющие простую физическую природу и допускающие непосредственное измерение (давление 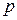, температура 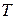, объем системы 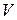), используют в качестве параметров состояния. Уравнением состояния называют выражение, связывающее эти параметры. Для однородных систем постоянного состава оно имеет вид

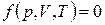(20.5)

У идеальных газов особенно простое уравнение состояния

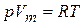, (20.6)

где 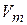– объем одного моля; – универсальная газовая постоянная.

Используя определение теплоемкости (20.3), первое начало термодинамики и уравнение состояния для газов, можно записать для идеальных газов в расчете на один моль:

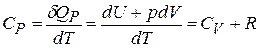, (20.7)

так как 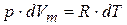при . Уравнение (20.7) называют соотношением Майера.

Если применить первое начало термодинамики (20.1) для описания адиабатического расширения (сжатия) идеального газа ( ; изменение состояния без теплообмена), учитывая определения:

, ,

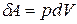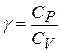соотношение Майера и введя обозначение (адиабатическая постоянная), то получим уравнение

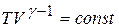(20.8)

Из него следует, что при адиабатическом процессе температура 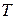и объем 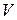идеального газа меняются таким образом, что произведение 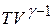остается постоянным. Поскольку 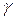всегда больше единицы, то 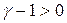и, адиабатическое расширение сопровождается охлаждением, а сжатие – нагреванием газа. Комбинируя уравнение (20.8) с (20.6), можно получить соотношение, связывающее параметры 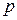и 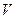при адиабатическом процессе

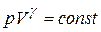(20.9)

Это равенство называется уравнением Пуассона. Еще одно уравнение для адиабатического процесса связывает параметры 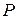и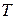

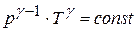
Величина 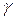для газов играет большую роль при адиабатических процессах. В частности, этой величиной определяется скорость распространения звука в газах; от нее зависит течение газов по трубам со звуковыми скоростями.