Теоретическое введение. В данной работе изучаются физические величины, характеризующие течение реальной жидкости
В данной работе изучаются физические величины, характеризующие течение реальной жидкости. Реальная жидкость отличается от идеальной тем, что она обладает внутренним трением, или вязкостью.
Если различные частицы жидкости движутся с одинаковыми скоростями, направленными одинаково, то это означает, что жидкость находится в равновесном состоянии. Однако, если скорость течения жидкости различна в разных местах, то такое состояние жидкости не является равновесным, и в ней возникают самопроизвольные процессы перехода в состояние равновесия. Эти процессы обуславливают появление особого свойства жидкости, которое называется вязкостью, или внутренним трением.
Рассмотрим плоскопараллельный поток жидкости, то есть такое ее течение, при котором векторы скорости 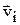 частиц жидкости всюду направлены одинаково. Пусть также модуль скорости
частиц жидкости всюду направлены одинаково. Пусть также модуль скорости 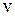 меняется (уменьшается) лишь
меняется (уменьшается) лишь  вдоль положительной оси
вдоль положительной оси 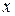 (рис. 18.1) перпендикулярной потоку жидкости (
(рис. 18.1) перпендикулярной потоку жидкости ( 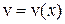 ). Опыт показывает, что соприкасающиеся слои жидкости, двигающиеся в одном и том же направлении, но с разными скоростями, воздействуют друг на друга. Сила взаимодействия ускоряет медленно движущийся элемент жидкости и замедляет более быстрый. Конечно, в сплошной среде никаких элементов жидкости нет и это понятие используется лишь для наглядности, а скорость жидкости распределена непрерывно. Если жидкость течет, соприкасаясь с твердой поверхностью (рис 18.1), то непосредственно прилегающий к твердой стенке слой жидкости “прилипает” к поверхности – скорость течения обращается в нуль на стенке. По мере удаления от стенки скорость жидкости увеличивается.
). Опыт показывает, что соприкасающиеся слои жидкости, двигающиеся в одном и том же направлении, но с разными скоростями, воздействуют друг на друга. Сила взаимодействия ускоряет медленно движущийся элемент жидкости и замедляет более быстрый. Конечно, в сплошной среде никаких элементов жидкости нет и это понятие используется лишь для наглядности, а скорость жидкости распределена непрерывно. Если жидкость течет, соприкасаясь с твердой поверхностью (рис 18.1), то непосредственно прилегающий к твердой стенке слой жидкости “прилипает” к поверхности – скорость течения обращается в нуль на стенке. По мере удаления от стенки скорость жидкости увеличивается.
Из опыта следует, что сила внутреннего трения 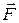 пропорциональна изменению скорости жидкости
пропорциональна изменению скорости жидкости 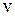 в направлении, перпендикулярном движению, и зависит от площади
в направлении, перпендикулярном движению, и зависит от площади 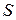 соприкосновения элементов жидкости. Быстрота изменения скорости
соприкосновения элементов жидкости. Быстрота изменения скорости 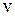 вдоль оси
вдоль оси 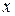 характеризуется производной
характеризуется производной 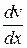 . Окончательный результат можно записать в виде:
. Окончательный результат можно записать в виде:
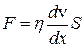 . (18.1)
. (18.1)
Это – закон вязкого трения Ньютона. Здесь 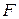 – величина силы, действующей со стороны одного слоя на другой,
– величина силы, действующей со стороны одного слоя на другой, 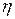 – коэффициент пропорциональности, получивший название коэффициента вязкости жидкости (динамическая вязкость). Он численно равен силе вязкого трения между слоями единичной площади при единичном градиенте скорости направленного движения слоёв. Его размерность вытекает из формулы (18.1). Единицу измерения принято выражать как 1 Па×с. Направление силы
– коэффициент пропорциональности, получивший название коэффициента вязкости жидкости (динамическая вязкость). Он численно равен силе вязкого трения между слоями единичной площади при единичном градиенте скорости направленного движения слоёв. Его размерность вытекает из формулы (18.1). Единицу измерения принято выражать как 1 Па×с. Направление силы 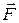 (вправо или влево на рис. 18.1) зависит от того, быстрее или медленнее движутся слои относительно друг друга.
(вправо или влево на рис. 18.1) зависит от того, быстрее или медленнее движутся слои относительно друг друга.
Коэффициент вязкости 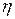 имеет разные значения для различных жидкостей, а для определенной жидкости зависит от внешних условий, в первую очередь от температуры. По своей природе силы трения в жидкости являются силами межмолекулярного взаимодействия, т.е электромагнитными силами, как и силы трения между твердыми телами.
имеет разные значения для различных жидкостей, а для определенной жидкости зависит от внешних условий, в первую очередь от температуры. По своей природе силы трения в жидкости являются силами межмолекулярного взаимодействия, т.е электромагнитными силами, как и силы трения между твердыми телами.
Процесс выравнивания скоростей между соседними слоями жидкости сопровождается переносом импульса 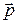 от слоя к слою. Механизм этого переноса имеет молекулярный характер. Коэффициент вязкости и определяет быстроту передачи импульса из одного места в другое при течении жидкости. В соответствии со вторым законом Ньютона взаимодействие слоев жидкости с силой
от слоя к слою. Механизм этого переноса имеет молекулярный характер. Коэффициент вязкости и определяет быстроту передачи импульса из одного места в другое при течении жидкости. В соответствии со вторым законом Ньютона взаимодействие слоев жидкости с силой 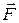 можно рассматривать как процесс передачи импульса из одного слоя в другой; сила равна быстроте переноса импульса
можно рассматривать как процесс передачи импульса из одного слоя в другой; сила равна быстроте переноса импульса 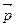 :
:
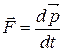 . (18.2)
. (18.2)
Благодаря вязкости жидкости возникает поток импульса 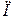 , равный по определению импульсу, переносимому за единицу времени через единичную площадку:
, равный по определению импульсу, переносимому за единицу времени через единичную площадку:
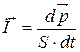 . (18.3)
. (18.3)
Из (18.1), (18.2) и (18.3) величина потока импульса равна
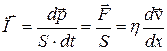 ,
,
или в проекциях
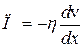 . (18.4)
. (18.4)
Знак «–» показывает, что импульс переносится из быстрого слоя в более медленный, то есть противоположно направлению градиента скорости слоёв.
Кроме динамической вязкости 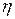 вводится также кинематическая вязкость
вводится также кинематическая вязкость 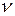 , которая характеризует быстроту выравнивания скорости течения жидкости. Импульс
, которая характеризует быстроту выравнивания скорости течения жидкости. Импульс 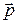 – динамическая характеристика движения. Он входит в основное уравнение динамики (18.2), а скорость – кинематическая характеристика и она равна импульсу, деленному на массу. Поэтому
– динамическая характеристика движения. Он входит в основное уравнение динамики (18.2), а скорость – кинематическая характеристика и она равна импульсу, деленному на массу. Поэтому 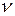 вводят таким образом
вводят таким образом
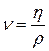 , (18.5)
, (18.5)
где 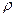 – плотность жидкости.
– плотность жидкости.
Представленные соотношения позволяют рассмотреть задачу о вычислении расхода несжимаемой жидкости, текущей в горизонтальной круглой прямолинейной трубе с постоянной площадью поперечного сечения при заданном перепаде давлений 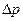 .
.
Эта задача имеет большое практическое значение: организация работы нефтепроводов, обычного водопровода безусловно требует ее решения. Будем полагать, что нам заданы длина трубы 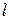 , ее радиус
, ее радиус  , давление на концах трубы
, давление на концах трубы 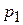 и
и 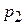 (
( 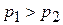 ), а также плотность жидкости
), а также плотность жидкости 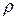 и ее вязкость
и ее вязкость 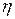 .
.
 Из решения этой задачи следует (см. лабораторную работу 1-17), что текущая в трубе жидкость имеет параболический профиль скоростей: скорость меняется в зависимости от расстояния
Из решения этой задачи следует (см. лабораторную работу 1-17), что текущая в трубе жидкость имеет параболический профиль скоростей: скорость меняется в зависимости от расстояния 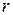 до оси трубы по квадратичному закону
до оси трубы по квадратичному закону
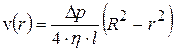 , (18.6)
, (18.6)
равна нулю на стенке и максимальна 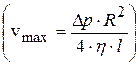 в центре трубы (рис.18.2). Здесь
в центре трубы (рис.18.2). Здесь 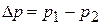 .
.
Объёмным расходом жидкости 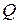 называется объём жидкости, протекающей по трубе за единицу времени. Он равен
называется объём жидкости, протекающей по трубе за единицу времени. Он равен
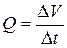 . (18.7)
. (18.7)
По формуле Пуазейля, вывод которой дан в лабораторной работе 1-17,
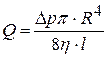 . (18.8)
. (18.8)
Отличительной чертой (18.8) является сильная зависимость от радиуса трубы: 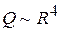 .
.
Рассмотренное течение жидкости по трубе характерно своей упорядоченностью и плавностью: каждая частица жидкости движется по определенной прямолинейной траектории, и вся картина течения представляет собой как бы движение различных слоев жидкости с различными скоростями друг относительно друга. Такое правильное, стационарное течение жидкости называют ламинарным (слоистым). Формула Пуазейля применима только для ламинарного течения жидкости.
При достаточно больших скоростях ламинарное течение становится неустойчивым, хаотичным и переходит в так называемое турбулентное течение (от латинских lamina – “пластина”, turbulentus – “бурный”, “беспорядочный”). Представление о турбулентном течении можно получить, если постепенно открывать водопроводный кран: тонкая струйка течет сначала плавно, но с увеличением скорости плавность течения нарушается, частицы жидкости перемещаются уже беспорядочно, и движение сопровождается сильным перемешиванием.
Для того, чтобы оценить характер течения жидкости, вводится безразмерная величина 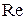 , называемая числом Рейнольдса.
, называемая числом Рейнольдса.
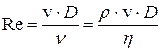 (18.9)
(18.9)
Здесь 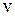 – средняя скорость потока,
– средняя скорость потока, 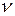 – кинематическая вязкость,
– кинематическая вязкость, 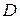 – характерный размер (в случае течения жидкости в трубе это диаметр трубы
– характерный размер (в случае течения жидкости в трубе это диаметр трубы 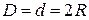 ). Опытные данные показывают, что существует критическое число Рейнольдса, при превышении которого происходит переход из ламинарного режима в турбулентный. Но сама величина
). Опытные данные показывают, что существует критическое число Рейнольдса, при превышении которого происходит переход из ламинарного режима в турбулентный. Но сама величина 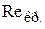 не универсальна – она зависит от геометрии системы. Для случая течения жидкости в трубе
не универсальна – она зависит от геометрии системы. Для случая течения жидкости в трубе 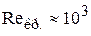 .
.
Дата добавления: 2015-03-19; просмотров: 727;
