Теоретическое введение. Газы отличаются от упругих тел тем, что они оказывают сопротивление изменению объема (но не формы)

Газы отличаются от упругих тел тем, что они оказывают сопротивление изменению объема (но не формы). Они всегда оказывают давление, стремясь расшириться и занять любой предоставленный объем.

Если газ не находится в состоянии покоя, т.е. равновесие отсутствует, то говорят, что имеется поток газа, и состояние движущегося газа полностью определено, если известна скорость потока в каждой точке пространства в каждый момент времени. Газ рассматриваем как сплошную среду. Для неустановившегося движения газа следует различать два способа описания: вводятся траектории, т.е. пути описываемые частицами газа с течением времени, и линии тока, которые получаются следующим образом. Представим себе, что в определенный момент в каждой точке потока в виде маленьких стрелок нарисованы векторы скорости частиц. Эти стрелки можно соединить кривыми, касательные к которым в каждой точке направлены вдоль стрелок. В неустановившемся потоке картина линий тока меняется со временем, и траектории частиц газа и линии тока не совпадают. В часто встречающихся на практике задачах рассматривается установившееся движение газа (стационарный поток), когда вектор скорости в каждой точке не меняется со временем, а линии тока совпадают с траекториями частиц. Примером стационарного потока является ламинарное течение. Ламинарным называется поток, в котом газ течет как бы параллельными слоями, скользящими друг относительно друга с различной скоростью. В простейшем случае все слои движутся в одинаковом направлении, например, вдоль оси 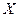. Из-за взаимодействия между слоями (это взаимодействие называется еще внутренним трением) более быстротекущий слой оказывает воздействие на прилегающий к нему слой, пытаясь увлечь его за собой. И наоборот, более медленно текущий слой тормозит более быстрый. Уже Ньютон указал правильный вид этой тормозящей силы: она должна быть пропорциональна площади 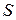соприкасающихся слоев и спаду скорости в перпендикулярном к потоку направлении. Следовательно, если скорость 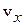уменьшается в направлении оси 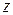(рис. 17.1), то на каждый слой действует прилегающий к нему слой с касательной силой, равной по величине

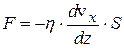(17.1)

Коэффициент пропорциональности 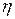называется коэффициентом внутреннего трения или коэффициентом вязкости.

Ламинарный параллельный поток имеет место, например, при медленном протекании газа в цилиндрической трубе (капилляре) – в этом случае слои представляют собой совокупность бесконечно тонких цилиндрических поверхностей, вложенных одна в другую, имеющих общую ось, совпадающую с осью трубы.

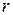Выделим в капилляре воображаемый цилиндрический объем газа радиусом и длиной 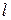, как показано на рисунке 17.2. Обозначим давления на его торцах 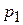и 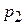. При установившемся течении суммарная сила давления на цилиндр

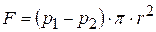
уравновесится силой внутреннего трения , которая действует на боковую поверхность цилиндра со стороны внешних слоев газа:

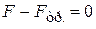. (17.2)

Сила внутреннего трения определяется по формуле Ньютона (17.1). Учитывая, что 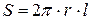(площадь поверхности цилиндра) и скорость 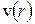уменьшается при удалении от оси трубы, т.е. 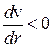, можно записать:

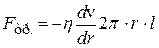(17.3)

В этом случае условие стационарности (17.2) запишется в виде:

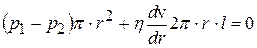(17.4)

Интегрируя это равенство, получим

,

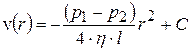где 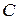– постоянная интегрирования, которая определяется граничными условиями задачи. При 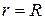скорость газа должна обратиться в нуль 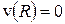, поскольку сила внутреннего трения о стенку капилляра тормозит смежный с ней слой газа. Тогда

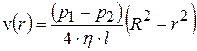(17.5)

Подсчитаем объемный расход газа 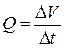, т.е. объем, который протекает за единицу времени через поперечное сечение трубы. Через кольцевую площадку с внутренним радиусом 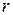и внешним 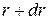за время 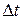протекает объем газа, равный произведению площади этой кольцевой площадки 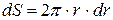на перемещение частиц газа за это время :

;

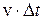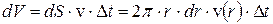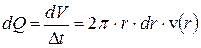
Тогда

;

,

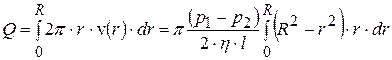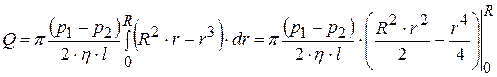
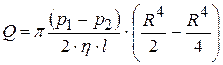или

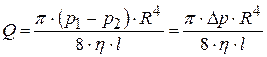(17.6)

Формулу (17.6), которая называется формулой Пуазейля, можно использовать для экспериментального определения коэффициента вязкости газа.

Формула Пуазейля была получена в предположении ламинарного течения газа или жидкости. Однако с увеличением скорости потока движение становится турбулентным и слои смешиваются. При турбулентном движении скорость в каждой точке меняет свое значение и направление, сохраняется только среднее значение скорости. Характер движения жидкости или газа в трубе определяется числом Рейнольдса:

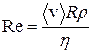, (17.7)

где 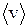– средняя скорость потока; 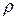– плотность жидкости или газа.

В гладких цилиндрических каналах переход от ламинарного течения к турбулентному происходит при 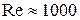. Поэтому в случае использования формулы Пуазейля необходимо обеспечить выполнение условия 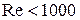. Кроме этого, эксперимент необходимо проводить таким образом, чтобы сжимаемостью газа можно было пренебречь. Это возможно тогда, когда перепад давлений вдоль капилляра значительно меньше самого давления. В данной установке давление газа несколько больше атмосферного ( см водяного столба), а перепад давлений составляет от ~ 10 см вод.ст., т.е. приблизительно 1% от атмосферного.

Формула (17.6) справедлива для участка трубы, в котором установилось постоянное течение с квадратичным законом распределения скоростей (17.5) по сечению трубы. Такое течение устанавливается на некотором расстоянии от входа в капилляр, поэтому для достижения достаточной точности эксперимента необходимо выполнение условия 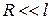, где – радиус, 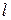– длина капилляра.