Методика измерений. Этот метод основан на измерении скорости установившегося движения твердого шарика в вязкой среде под действием постоянной внешней силы

Этот метод основан на измерении скорости установившегося движения твердого шарика в вязкой среде под действием постоянной внешней силы, в простейшем случае – силы тяжести.

Выведем рабочую формулу для определения коэффициента вязкости методом Стокса. Если взять шарик большей плотности, чем плотность жидкости, то он будет тонуть, опускаясь на дно сосуда. На падающий шарик действуют три силы (рис.16.3):

1. сила вязкого трения F_С по закону Стокса (16.6), направленная вверх, навстречу скорости: ;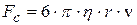

2. сила тяжести, направленная вниз:

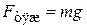, (16.7)

где 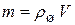– масса шарика; 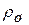– плотность шарика; 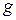– ускорение свободного падения; 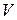– объем шарика, равный:

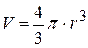; (16.8)

3. выталкивающая сила F_Арх, согласно закону Архимеда, равная весу вытесненной жидкости:

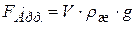, (16.9)

где 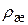– плотность жидкости.

Запишем уравнение движения (второй закон Ньютона) для падающего шарика в проекциях на вертикальную ось:

ma=F_тяж–F_Арх–F_С. (16.10)

Сила тяжести и выталкивающая сила не зависят от скорости движения шарика. Сила трения в законе Стокса прямо пропорциональна скорости. Поэтому на некотором начальном участке l₀ (рис.16.3) падения шарика в жидкости, пока скорость мала, сила трения меньше разности сил тяжести и выталкивающей, и шарик в результате движется с ускорением. Величину участка 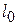можно оценить из уравнения движения.

По мере нарастания скорости падения шарика растет сила вязкого трения. С момента достижения равенства

F_С = F_тяж – F_Арх (16.11)

сумма сил, действующих на шарик, становится равной нулю, и шарик, в соответствии с первым законом Ньютона, движется по инерции равномерно, с набранной им к этому моменту скоростью. По измеренной скорости установившегося падения шарика можно найти коэффициент вязкости жидкости η.

После подстановки в (16.11) выражений (16.6-16.9) получим:

.

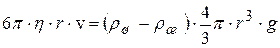Сократим на радиус 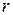и сделаем замену 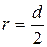( 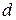– диаметр шарика):

;

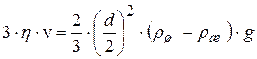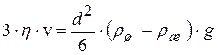. (16.12)

Из (16.12) выразим коэффициент динамической вязкости:

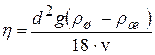. (16.13)

Далее скорость v шарика выражаем через пройденный путь 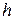и время падения : :

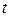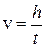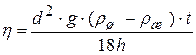. (16.14)

Выведенная формула (16.14) для расчета коэффициента вязкости, как и формула Стокса (16.6), получены в предположении, что шарик движется в сосуде неограниченного объема.