Теоретическое введение. Колебательным движением называется процесс, при котором система, многократно отклоняясь от положения равновесия
 Колебательным движением называется процесс, при котором система, многократно отклоняясь от положения равновесия, каждый раз вновь возвращается к нему.
Колебательным движением называется процесс, при котором система, многократно отклоняясь от положения равновесия, каждый раз вновь возвращается к нему.
Существует общность закономерностей большого разнообразия колебательных процессов, поэтому все они могут быть сведены к совокупности простейших колебаний – гармонических.
Гармоническим колебательным движением называется такое колебательное движение, при котором колеблющаяся величина изменяется с течением времени по закону синуса или косинуса. Основные характеристики колебательных процессов можно рассмотреть на примере механических колебаний материальной точки.
Представим себе материальную точку М, равномерно вращающуюся по окружности радиуса А с угловой скоростью ω (рис.12.1). Тогда точка Мх – проекция точки М на ось х – будет совершать периодические колебания вдоль оси х. Смещение колеблющейся точки от положения равновесия вдоль оси х определяется по закону:
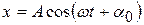 , (12.1)
, (12.1)
где А – амплитуда колебаний (абсолютное значение максимального смещения), 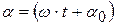 – фаза колебаний, которая определяет угловое смещение точки М в любой момент времени, α0 – начальная фаза,
– фаза колебаний, которая определяет угловое смещение точки М в любой момент времени, α0 – начальная фаза, 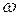 – круговая (циклическая) частота, равная
– круговая (циклическая) частота, равная
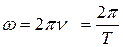 ; (12.2)
; (12.2)
ν – частота колебаний (число полных колебаний в единицу времени, 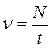 ,
, 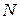 – число колебаний за время t),
– число колебаний за время t), 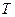 – период колебаний (время совершения одного полного колебания). Выражение (12.1) – кинематическое уравнение гармонического колебательного движения.
– период колебаний (время совершения одного полного колебания). Выражение (12.1) – кинематическое уравнение гармонического колебательного движения.
 Скорость
Скорость 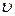 колеблющейся материальной точки получим, продифференцировав (12.1) по времени:
колеблющейся материальной точки получим, продифференцировав (12.1) по времени:
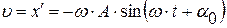 . (12.3)
. (12.3)
Продифференцировав (12.3), получим ускорение а:
 . (12.4)
. (12.4)
Учитывая (12.1), имеем: 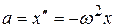 , или:
, или:
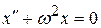 . (12.5)
. (12.5)
Выражение (12.5) описывает гармонические колебания величины x и называется дифференциальным уравнением гармонического осциллятора. Его решением является гармоническая функция (12.1). Если вторая производная по времени какой-либо физической величины (не обязательно смещения) пропорциональна самой величине с противоположным знаком, то данная физическая величина изменяется со временем по гармоническому закону.
Любое тело (рис. 12.2), подвешенное в поле силы тяжести так, что точка подвеса О не совпадает с центром тяжести С, называется физическим маятником. Пусть отклонение маятника от положения равновесия характеризуется углом φ. При отклонении маятника от положения равновесия возникает вращающий момент силы 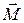 , стремящийся вернуть маятник в положение равновесия. Его величина
, стремящийся вернуть маятник в положение равновесия. Его величина 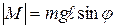 , где m – масса маятника;
, где m – масса маятника; 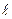 – расстояние от центра тяжести маятника до точки подвеса,
– расстояние от центра тяжести маятника до точки подвеса, 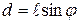 – плечо силы тяжести (кратчайшее расстояние от линии действия силы до оси вращения).
– плечо силы тяжести (кратчайшее расстояние от линии действия силы до оси вращения).
Направления вращающего момента 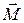 и углового перемещения
и углового перемещения 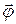 противоположны (момент силы возвращает маятник к положению равновесия), поэтому в проекциях на ось вращения
противоположны (момент силы возвращает маятник к положению равновесия), поэтому в проекциях на ось вращения
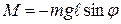 . (12.6)
. (12.6)
По второму закону Ньютона для вращательного движения маятника:
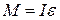 , (12.7)
, (12.7)
где 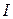 – момент инерции маятника относительно оси, проходящей через точку подвеса; e – угловое ускорение маятника, равное второй производной угла поворота:
– момент инерции маятника относительно оси, проходящей через точку подвеса; e – угловое ускорение маятника, равное второй производной угла поворота: 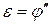 .
.
Из уравнений (12.6) и (12.7) имеем:
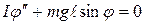 , или
, или 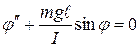 . (12.8)
. (12.8)
При малых углах 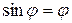 , и уравнение (12.8) будет иметь вид:
, и уравнение (12.8) будет иметь вид:
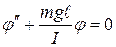 . (12.9)
. (12.9)
Сравнивая (12.9) и (12.5), устанавливаем, что j изменяется по гармоническому закону с круговой частотой ω, причем

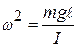 , (12.10)
, (12.10)
а период колебаний маятника
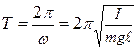 . (12.11)
. (12.11)
Частным случаем физического маятника является маятник математический. Если вся масса маятника сосредоточена в одной точке (например, шарик, подвешенный на невесомой нерастяжимой нити), то такой маятник называют математическим (рис.12.3). Для математического маятника момент инерции рассчитывается как для материальной точки: 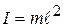 , поэтому период его колебаний равен:
, поэтому период его колебаний равен:
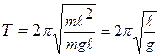 . (12.12)
. (12.12)
Формулу (12.12) можно получить, непосредственно записав второй закон Ньютона для материальной точки. На шарик, подвешенный на нити (рис.12.3), действуют сила тяжести 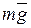 и сила натяжения нити
и сила натяжения нити 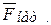 , тогда
, тогда
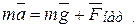 . (12.13)
. (12.13)
Сила натяжения нити 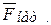 не имеет касательной составляющей, а проекция силы тяжести для малых углов φ равна
не имеет касательной составляющей, а проекция силы тяжести для малых углов φ равна 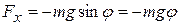 , тогда касательное ускорение
, тогда касательное ускорение 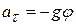 . Угол отклонения маятника из положения равновесия
. Угол отклонения маятника из положения равновесия 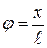 , где x – отклонение из положения равновесия. Наконец, касательное ускорение – это вторая производная координаты x, тогда
, где x – отклонение из положения равновесия. Наконец, касательное ускорение – это вторая производная координаты x, тогда
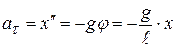 . (12.14)
. (12.14)
Отсюда 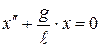 . Это дифференциальное уравнение гармонических колебаний идентично (12.5), если
. Это дифференциальное уравнение гармонических колебаний идентично (12.5), если 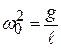 ; следовательно, (12.12) доказано.
; следовательно, (12.12) доказано.
Приведенной длиной физического маятника называется длина такого математического маятника, который имеет тот же период колебаний, что и данный физический маятник:
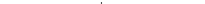
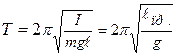 . (12.15)
. (12.15)
В лабораторной работе используется физический маятник в виде кольца (рис.12.4) или в виде однородного тонкого стержня (рис.12.5). Момент инерции маятника относительно точки подвеса О можно найти по теореме Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельно данной оси, и произведения массы тела на квадрат расстояния между осями. Для кольца получим:
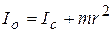 . (12.16)
. (12.16)
Здесь 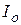 – момент инерции маятника относительно оси, проходящей через точку подвеса O, IC – момент инерции относительно оси, проходящей через центр масс – точку C, r – расстояние между осями. Момент инерции полого (толстостенного) цилиндра или кольца массой m с внутренним радиусом r и наружным R относительно оси, проходящей через центр масс, равен:
– момент инерции маятника относительно оси, проходящей через точку подвеса O, IC – момент инерции относительно оси, проходящей через центр масс – точку C, r – расстояние между осями. Момент инерции полого (толстостенного) цилиндра или кольца массой m с внутренним радиусом r и наружным R относительно оси, проходящей через центр масс, равен:
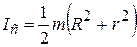 , (12.17)
, (12.17)
Тогда из (12.16) и (12.17) получаем:
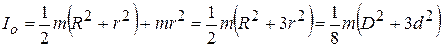 , (12.18)
, (12.18)
где 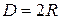 и
и 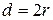 – внешний и внутренний диаметры кольца соответственно. Из (12.11) выразим ускорение свободного падения с учетом, что длина физического маятника равна расстоянию от точки подвеса до центра масс, то есть для кольца
– внешний и внутренний диаметры кольца соответственно. Из (12.11) выразим ускорение свободного падения с учетом, что длина физического маятника равна расстоянию от точки подвеса до центра масс, то есть для кольца 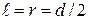 , и из (12.18) подставим момент инерции:
, и из (12.18) подставим момент инерции:
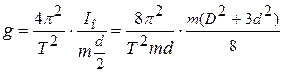 ,
,
и окончательно:
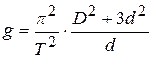 . (12.19)
. (12.19)
Для стержня по теореме Штейнера получим:

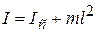 , (12.20)
, (12.20)
|
|
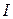 – момент инерции стержня относительно точки подвеса О,
– момент инерции стержня относительно точки подвеса О, 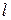 – расстояние между центром масс (центром стержня) и точкой подвеса (длина физического маятника),
– расстояние между центром масс (центром стержня) и точкой подвеса (длина физического маятника), 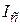 – момент инерции стержня относительно центра масс:
– момент инерции стержня относительно центра масс:
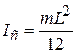 , (12.21)
, (12.21)
L – длина стержня, m – его масса. Можно показать, что для любого маятника приведенная длина lпр. больше, чем расстояние 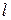 от центра масс до точки подвеса (длины физического маятника): из (12.15) и (12.20) следует, что
от центра масс до точки подвеса (длины физического маятника): из (12.15) и (12.20) следует, что
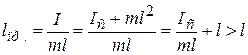 .
.
Точка О1, лежащая на прямой ОС на расстоянии lпр.от точки подвеса маятника (рис.12.5), называется центром качания маятника. Центр качания О1 и точка подвеса О обладают свойством взаимности: если маятник подвесить так, чтобы его ось качания проходила через точку О1, то точка О будет совпадать с новым положением центра качания маятника, то есть приведенная длина и период колебаний маятника останутся прежними. Покажем это. По теореме Штейнера момент инерции I1 маятника относительно оси, проходящей через точку О1, равен:
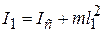 . (12.22)
. (12.22)
Из (12.20) и (12.22) вычислим 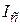 :
:
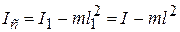 . (12.23)
. (12.23)
Из (12.10) выразим момент инерции маятника 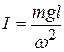 и запишем аналогичную формулу для
и запишем аналогичную формулу для 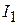 :
: 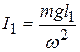 . Здесь использовано условие, что частота колебаний маятника относительно оси, проходящей через точку О1, должна быть той же самой, что и для оси, проходящей через точку О. Подставив оба момента инерции в (12.23) получим уравнение:
. Здесь использовано условие, что частота колебаний маятника относительно оси, проходящей через точку О1, должна быть той же самой, что и для оси, проходящей через точку О. Подставив оба момента инерции в (12.23) получим уравнение:
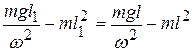 .
.
Далее после преобразований: 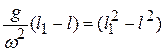 ; и после сокращения на
; и после сокращения на 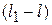 получим:
получим: 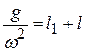 . По определению приведенной длины физического маятника (12.15):
. По определению приведенной длины физического маятника (12.15): 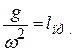 , то есть
, то есть 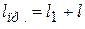 , что и требовалось показать.
, что и требовалось показать.
Для физического маятника – стержня из (12.15), (12.20) и (12.21):
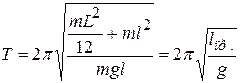 , или
, или
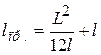 . (12.24)
. (12.24)
Дата добавления: 2015-03-19; просмотров: 906;
