Недостаточность модели 2

При выводе формулы (11.20) предполагали, что растяжение пружины равномерное. При каком условии это допущение приемлемо? Естественно считать, что это можно сделать, если характерное время τ, связанное с собственными продольными колебаниями пружины, существенно меньше характерного времени, связанного с колебаниями груза (например, периода колебаний T):

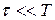. (11.21)

В этом случае неравномерность растяжения пружины будет успевать выравниваться за период колебаний. За τ можно принять время прохождения возмущения вперед и назад вдоль пружины:

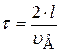, (11.22)

где 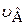– скорость распространения упругих волн по пружине. Для её оценки

воспользуемся выражением, определяющим скорость распространения продольных звуковых волн в твердых телах:

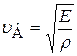, (11.23)

где 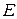– модуль Юнга, ρ – плотность среды. Для твёрдого тела, например, стержня длиной l и сечением S (см. лаб. работу 1-14):

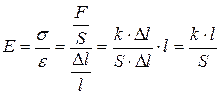, (11.24)

а плотность

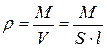, (11.25)

тогда

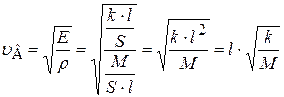. (11.26)

Таким образом, допущение о равномерном растяжении пружины можно считать приемлемым, если

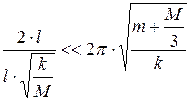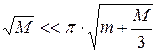, или . (11.27)

Допустив, что «значительно меньше» означает «меньше по крайней мере в 10 раз», получаем условие приемлемости допущения:

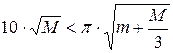. (11.28)

После возведения в квадрат и с учётом, что 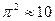: 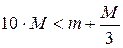. Далее, учитывая приблизительность выкладок, вторым слагаемым в правой части пренебрежём и получим:

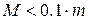. (11.29)

Требование (11.29) устраняет и ещё одно упрощение модели 2: если масса пружины велика, то она под действием собственного веса будет растягиваться неравномерно (вверху растянута больше, чем внизу), и соотношения (11.12) и (11.13) неверны. Однако можно предположить, что наличие поля силы тяжести не будет влиять на период колебаний, так же как и для маятника с безмассовой пружиной, а всего лишь изменит равновесное положение груза.

Следующий шаг в решении вопроса – это решение задачи на поиск частот нормальных колебаний (см. лаб. работу 2.10) системы, состоящей из точечного груза и пружины с непрерывно распределённой массой. Эта задача сложна, однако в простейшем частном случае её легко можно решить. Этот частный случай – колебания пружины массой M без груза (m=0).

Модель 3. Колебания массивной пружины без груза

На длине стержня должно укладываться полуцелое число длин стоячих волн:

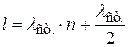, n=0, 1, 2, 3, … , (11.30)

где длина стоячей волны равна половине длины волны бегущей:

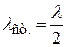. (11.31)

Воспользуемся (11.26), тогда с учётом (11.32):

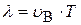, (11.32)

а также (11.30) и (11.31) получим выражение для периода T₀ основного тона колебаний (n=0) стержня:

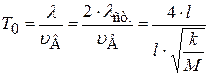, или 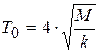. (11.33)

Сравним (11.20) и (11.33). При малом значении массы груза (m→0) (11.20) даёт:

.

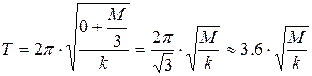Таким образом, в пределах погрешности 10% (11.20) и (11.33) дают одинаковый результат. Можно предположить, что область применимости (11.20) всё-таки шире, чем при 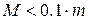. Это предположение предлагается проверить на опыте.

Экспериментальная часть

Приборы и оборудование: три пружины на штативе, набор грузов, линейка, секундомер.