Порядок выполнения работы. Задание 1. Определение жесткости пружины
Задание 1. Определение жесткости пружины
1. Вставьте линейку внутрь пружины 1 так, чтобы прорезь линейки опиралась на её нижний виток. При этом нижний виток пружины должен совпадать с нулём отсчёта линейки. Измерьте длину ненагруженной пружины l0.

2. Подвесьте к пружине груз массой m, запишите l – длину пружины с грузом.
3. Вычислите удлинение пружины 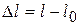 и вычислите её жёсткость k по закону Гука (11.34):
и вычислите её жёсткость k по закону Гука (11.34):
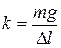 . (11.34)
. (11.34)
4. Повторите опыт ещё с двумя грузами.
5. Рассчитайте среднее значение коэффициента жёсткости kср.. Повторите измерения с пружинами 2 и 3. Все результаты занесите в таблицу 11.1.
Таблица 11.1
| Пружина 1 | ||||||
| № | l0, м | m, кг | l, м | 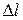 , м , м
| k, Н/м | kср., Н/м |
| 1.0 | ||||||
| 1.5 | ||||||
| 2.0 | ||||||
| Пружина 2 | ||||||
| № | l0, м | m, кг | l, м | 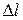 , м , м
| k, Н/м | kср., Н/м |
| 1.0 | ||||||
| 1.5 | ||||||
| 2.0 | ||||||
| Пружина 3 | ||||||
| № | l0, м | m, кг | l, м | 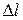 , м , м
| k, Н/м | kср., Н/м |
| 0.1 | ||||||
| 0.5 | ||||||
| 0.6 |
Задание 2. Определение периода свободных колебаний
1. Уберите линейку. Подвесьте к пружине 1 груз m=1 кг.
2. Приготовьте к работе секундомер, оттяните груз вниз. Отпустите маятник вместе с пуском секундомера. Отсчитайте N (N=20÷30) полных колебаний (считать число полных колебаний по моментам возвращения маятника в нижнее положение максимального отклонения). Запишите в табл.11.2 время t.
Таблица 11.2
| Пружина 1 M=0.94 кг | ||||||||||
| № | m, кг | N | t, с | T, с | 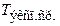 ,
с ,
с
| 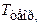 ,
с ,
с
| Е, % | 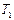 ,
с ,
с
| 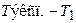 ,
с ,
с
| Е1, % |
| Пружина 2 M=0.53 кг | ||||||||||
| № | m, кг | N | t, с | T, с | 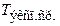 ,
с ,
с
| 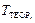 ,
с ,
с
| Е, % | 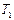 ,
с ,
с
| 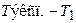 ,
с ,
с
| Е1, % |
| Пружина 3 M=0.09 кг | ||||||||||
| № | m, кг | N | t, с | T, с | 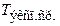 ,
с ,
с
| 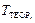 ,
с ,
с
| Е, % | 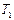 ,
с ,
с
| 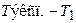 ,
с ,
с
| Е1, % |
| 0.5 | ||||||||||
3. Вычислите период колебаний: 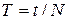 .
.
4. Повторите опыт (пункты 2 и 3) ещё 2 раза, рассчитайте среднее значение периода колебаний TСР.ЭКСП..
5. Найдите теоретическое значение периода 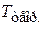 по формуле (11.20).
по формуле (11.20).
6. Оцените относительную погрешность, допускаемую при вычислении периода по формуле (11.20) с учётом массы пружины:
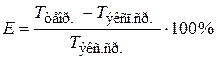 .
.
7. Найдите теоретическое значение периода колебаний маятника без учёта массы пружины по формуле (11.11):
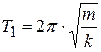 . (11.11)
. (11.11)
8. Вычислите разность 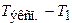 , оцените относительную погрешность Е1, допускаемую при вычислении периода колебаний по формуле (11.11) без учёта массы пружины:
, оцените относительную погрешность Е1, допускаемую при вычислении периода колебаний по формуле (11.11) без учёта массы пружины:
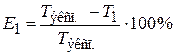 .
.
9. Повторите измерения и вычисления по пунктам 1-8 второго задания для пружин 2 и 3. Все полученные данные запишите в табл. 11.2.
10. Сделайте выводы о приемлемости модели 1 или 2 для каждой из исследованных пружин.
Контрольные вопросы
1. Какие колебания называются гармоническими? Дайте определение периода колебаний, частоты. Получите выражения для скорости и ускорения при механических гармонических колебаниях.
2. Запишите закон сохранения энергии для пружинного маятника в предположении, что массой пружины можно пренебречь.
3. Получите дифференциальное уравнение гармонических колебаний пружинного маятника (11.9).
4. Запишите решение уравнения (11.9), получите формулу для периода колебаний.
5. Выведите формулу для кинетической энергии колеблющейся пружины (11.15).
6. Получите и решите дифференциальное уравнение колебаний маятника с массивной пружиной.
7. Чему равен период колебаний маятника с массивной пружиной?
8. В каких случаях применима модель 2 маятника с массивной пружиной?
Используемая литература
[5] § 19.1, 19.2; [3] § 27.1, 27.2; [6] § 3.3; 3.6, 3.7.
Дата добавления: 2015-03-19; просмотров: 940;
