Оцінка ймовірного часу порушення електропостачання.

Параметр потоку відмов визначається з статистичних матеріалів спостережень над елементами системи електропостачання на протязі декількох років. Наприклад, якщо в установці були наявні вимикачів і на протязі 8 років було відмічено відмов, то параметр потоку відмов (середнє значення випадкової величини, чи математичне сподівання):

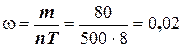рази/рік (7)

Для електричних мереж, відмови яких залежать від довжини лінії, параметр потоку відмов приймається рівним числу відмов (відключень) на протязі року, віднесеному до довжини мережі зазвичай на 100 км.

Величина залежить від строку служби елемента згідно кривої, характерної для більшості виробів (рис.1). Ділянка 1 відповідає періоду доробки чи наладку (зазвичай недовгому), ділянка 2 – періоду нормальної експлуатації і 3 – ділянка старіння виробу, коли параметр потоку відмов зростає за рахунок зношення, старіння ізоляції і т. ін.

Зазвичай розрахунки здійснюються для нормальної експлуатації (ділянка 2), коли параметр потоку відмов не змінюється протягом тривалого часу: =const.

Відмова характеризується законом розподілу випадкових величин, що виражає залежність ймовірності тієї чи іншої події в залежності від значення випадкової величини.

Рис.1 Залежність від часу t.

Для елементів систем електропостачання розподіл ймовірностей безвідмовної роботи елемента на протязі часу Т у більшості випадків підкоряється експоненціальному закону: 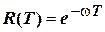. Наприклад ймовірність безвідмовної роботи комірки РП 10 кВ на протязі року при 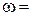0,02 рази/рік за час Т=1 год: .

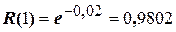При схемі електричної мережі, що складається з 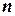послідовно з’єднаних елементів, ймовірність безвідмовної роботи мережі за час 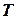визначається добутком імовірностей:

. (8)

При експоненціальному законі розподілу:

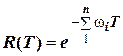. (9)

Таким чином, збільшення кількості послідовно ввімкнених елементів призводить до зниження надійності.

Перший важливий показник надійності роботи елементів системи електропостачання – середній час напрацювання між двома відмовами, його можна визначити за допомогою наступної формули:

. (10)

Другий важливий показник надійності роботи елементів систем електропостачання є час відновлення після відмови 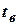. Оскільки час відновлення елементів є також випадковою величиною, необхідно знати, за яким законом розподілу розподіляється цей час. Закон знаходиться за допомогою статистичної обробки даних по відмовах елементів, об’єм яких повинен бути достатньо великим, щоби забезпечити необхідну точність результатів обробки. Середня його величина як і математичне сподівання випадкової величини 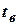для відмов:

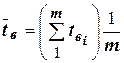. (11)

Якщо підприємство працює в одну чи в дві зміни, то час відновлення може накластись на неробочий період і не буде пов’язаний з збитками для виробництва. Якщо прийняти, що ймовірність відмов в різний час доби однакова, отримаємо значення часу відновлення, пов’язане з збитками:

. (12)

де 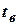– загальний час відновлення, 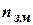– число змін.

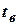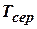При відомих і визначаються: коефіцієнт готовності системи:

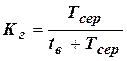, (13)

і коефіцієнт простою системи:

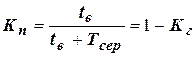. (14)

Системи електропостачання характеризуються високими коефіцієнтами готовності, близькими до одиниці, завдяки чому у більшості випадків можна обмежуватись для резервування другим паралельно ввімкненим елементом – двома лініями, двома трансформаторами і т. ін.

Якщо є мережа електропостачання, що складається з вимикачів, комірок РП, трансформаторів, кабельних чи повітряних ліній, з’єднаних послідовно, то для такої мережі можна визначити сумарне значення параметра потоку відмов:

, (15)

де 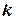– число елементів в мережі.

Середній час для відновлення електропостачання в годинах чи долях року:

. (16)

Час напрацювання мережі:

. (17)

В теорії надійності резервованих систем з відновленням показано, що при 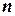паралельних вітках з однаковими характеристиками середній час порушення електропостачання системи при відмові всіх 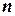мереж:

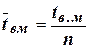. (18)

і час напрацювання системи між двома відмовами всіх віток:

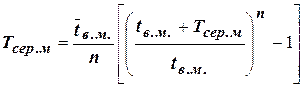. (19)

При двох вітках час відновлення системи:

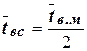. (20)

Час напрацювання системи:

. (21)

Розрахунки показують, що для споживачів ІІ категорії величина збитків при відключенні 1 раз в 25 років настільки незначна, що різниця в приведених затратах на подвійну мережу не оправдовується економією при збитках.

В експлуатації, крім простоїв при відмовах, мають місце профілактичні ремонти, тривалість яких співрозмірна з часом відновлення при відмовах. Виникає питання, наскільки ймовірна поява відмови в одній вітці при профілактичному ремонті іншої. В цьому випадку розглядаються ймовірності одночасних відмов обох віток і ймовірність накладання відмови однієї вітки на ремонт іншої. Очевидно, що накладання ремонту однієї вітки на відмову іншої виключається. Слід врахувати, що час ремонту мережі визначається максимальним часом ремонту одного елементу, так як на протязі цього часу всі інші елементи будуть відремонтовані.

Питання врахування ремонтів в розрахункові надійності пов’язаний з умовами виробництва. Для підприємств, що працюють з двома вихідними днями, здійснення ремонту не пов’язане з порушенням електропостачання. Ряд підприємств зупиняються на ремонт під час великих календарних свят при непервній роботі весь інший час. Є виробництва, що періодично зупиняють технологічне обладнання на профілактику, що полегшує ремонт електричної мережі.

Враховуючі всі ці обставини, а також дуже малу ймовірність накладання відмови однієї вітки на ремонт іншої, необхідно вважати, що в багатьох випадках простої через ремонт резервованих мереж враховувати не слід.

Якщо паралельні за схемою елементи розраховані не неповну пропускну здатність на покривання навантаження, то відмова будь-якого елементу в кожній вітці викликає одинакові наслідки в порушенні електропостачання. Тому з точки зору надійності ці елементи вважаються як би з’єднаними послідовно, і відповідно до цього підраховується середнє число відмов такої схеми з частковим порушенням електропостачання. Таким чином поняття послідовного і паралельного з’єднання в теорії надійності не відповідає поняттям в електротехніці.