Сущность множественного корреляционного метода, его применение в АХД и оценка результатов

Как правило, каждый фактор в отдельности не определяет изу­чаемые явления во всей полноте. Только комплекс факторов в их взаимосвязи может приблизительно дать представление о характере изучаемых явлений.

Метод множественной корреляции применяется в тех случаях, когда результативный показатель зависит от нескольких взаимно независимых факторов. Многофакторный корреляционный анализ со­стоит из нескольких этапов:

- на первом этапе определяются факторы, которые оказывают воздействие на результативный показатель, и отбираются наиболее существенные;

- на втором этапе собирается и оценивается исходная информа­ция, необходимая для корреляционного анализа;

- на третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, т. е. подбирается и обос­новывается математическое уравнение, которое наиболее точно вы­ражает сущность исследуемой зависимости;

- на четвертом этапе проводится расчет основных показателей связи корреляционного анализа;

- на пятом этапе дается статистическая оценка результатов кор­реляционного анализа и практического их применения.

1 этап. Отбор факторов для корреляционного анализа является важным моментом, и от того, насколько правильно отобраны факторы, зависят конечные результаты анализа.

При отборе факторов для корреляционного анализа необходимо придерживаться следующих правил.

1. В первую очередь следует учитывать причинно-следственные связи между показателями, так как только они раскрывают сущ­ность изучаемых явлений. Анализ же таких факторов, которые нахо­дятся только в математических соотношениях с результативным по­казателем, не имеет практического смысла.

2. При создании многофакторной корреляционной модели не­обходимо отбирать самые значимые факторы, которые оказывают решающее воздействие на результативный показатель, так как охва­тить все условия и обстоятельства практически невозможно. Факторы, которые имеют критерий надежности по Стьюденту меньше таблич­ного, не рекомендуется принимать в расчет.

3. Все факторы должны быть количественно измеримы, иметь единицу измерения, и информация о них должна содержаться в учете и отчетности.

4. В корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем имеет криволинейный и функциональный характер.

5. Не рекомендуется включать в корреляционную модель взаимо­связанные факторы. Если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного ана­лиза один из них необходимо исключить, иначе это приведет к ис­кажению результатов анализа.

При отборе факторов для корреляционной модели используют аналитические группировки, способ сравнения параллельных и дина­мических рядов, линейные графики, что позволяет определить нали­чие, направление и форму зависимости между изучаемыми показате­лями. Отбор факторов можно производить также в процессе решения задачи корреляционного анализа на основе оценки их значимости по критерию Стьюдента.

2этап. Проверка собранной для анализа информации на достоверность, однородность и соответствие закону нормально­го распределения. В первую очередь необходимо убедиться в досто­верности информации, т. е. насколько она соответствует объектив­ной действительности. Использование недостоверной информации приведет к неточным результатам анализа и к неправильно принято­му управленческому решению.

Одно из условий корреляционного анализа - это однород­ность исходной информации относительно ее распределения во­круг среднего уровня показателей. Если в совокупности имеются группы объектов, значительно отличающиеся от среднего уровня показателей, то это свидетельствует о неоднородности исходной информации.

Критерием однородности информации являются среднеквадратическое отклонение и коэффициент вариации, которые рассчи­тываются по каждому факторному и результативному показателям.

Среднеквадратическое отклонение показывает абсолютное отклонение приведенных значений от среднеарифметической вели­чины и определяется следующим образом:

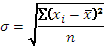
Коэффициент вариации показывает относительную меру от­клонения отдельных значений от среднеарифметической и рассчи­тываются следующим образом:

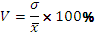
Чем больше коэффициент вариации, тем относительно больший разброс и меньшая выраженность исследуемых объектов.

3 этап. Проводится моделирование связи между факторными и результативным показателями после отбора факторов и оценки исходной информации т.е. подбирается соответствующее уравнение, которое наилучшим образом описывает изучаемые зависимости. Для его обоснования используются аналитические группировки, линейные графики.

Если связь всех факторных показателей с результативным носит прямолинейный характер, то для задания данной зависимости можно использовать линейную функцию:

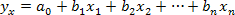
В случае криволинейного характера связи между результативным и факторными показателями может быть использована степенная или логарифмическая функция:

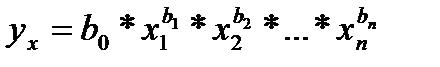
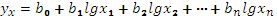
Данные модели позволяют дать экономическую интерпретацию па­раметрам 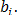В первой линейной модели коэффициенты 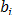показывают, на сколько единиц изменяется результативный показатель с изменением факторного показателя на единицу в абсолютном выражении, в степен­ных и логарифмических моделях - в процентах.

В случае, когда трудно обосновать форму зависимости, решение задачи можно провести по разным моделям с применением типовых программ на ПЭВМ и сравнить полученные результаты. Для этого вначале формируется матрица исходных данных, в которой первая колонка отражает порядковый номер наблюдения, вторая - значения результативного показателя, последняя - значения факторных показа­телей. Данные сведения заносятся в ПЭВМ и на их основании рассчи­тываются матрицы парных и частных коэффициентов корреля­ции, уравнение множественной регрессии, а также показатели оценки надежности коэффициентов корреляции и уравнения связи. Значи­мость коэффициентов корреляции проверяется по критерию Стьюдента.

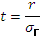
где 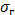– средняя квадратическая ошибка коэффициента корреляции, которая определяется по формуле:

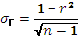
Для оценки точности (надежности) уравнения связи и право­мерности его использования для практических целей дается стати­стическая оценка надежности показателей связи. Для этого использу­ются критерий Фишера (F-отношение), средняя ошибка аппроксима­ции, коэффициенты множественной корреляции и детерминации.

Коэффициенты парной корреляции характеризуют тесноту связи между двумя показателями в общем виде с учетом взаимодействия с ос­тальными факторами, определяющими уровень результативного показа­теля. Для нейтрализации воздействия других факторов на ре­зультативный показатель рассчитываются частные коэффициенты кор­реляции. Таким образом, с помощью парных и частных коэффициентов корреляции можно получить представление о степени связи между изу­чаемыми явлениями в общих и непосредственных соприкосновениях.

4 этап. Расчет уравнения связи (регрессии) проводится, как пра­вило, шаговым способом. Вначале в расчет принимается один фактор, который оказывает наиболее значимое влияние на результативный по­казатель, потом второй, третий и т. д. На каждом шаге рассчитывается уравнение связи, множественный коэффициент корреляции и детерми­нации, F - отношение, стандартная ошибка и другие показатели, с помо­щью которых оценивается надежность уравнения связи. Величина их на каждом шаге сравнивается с предыдущей величиной. Чем выше вели­чина коэффициентов множественной корреляции, детерминации и кри­терии Фишера и чем ниже величина стандартной ошибки, тем точнее уравнение связи описывает зависимости, сложившиеся между иссле­дуемыми показателями. Если добавление следующих факторов не улучшает оценочных показателей связи, то их надо отбросить, т. е. ос­тановиться на том уравнении, где эти показатели оптимальны.

Коэффициенты уравнения показывают количественное воздействие каждого фактора на результативный показатель при неизменности дру­гих и могут иметь разные единицы измерения, что делает их несопоста­вимыми, если возникает вопрос о сравнительной силе воздействия фак­торов на результативный показатель. Чтобы привести их в сопостави­мый вид, все переменные уравнения регрессии выражают в долях среднеквадратического отклонения, т.е. рассчитывают стандартизованные коэффициенты регрессии, называемые бета-коэффициентами.

Бета-коэффициенты связаны следующим отношением:

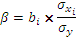
Бета-коэффициенты показывают, что если величина фактора уве­личится на одно среднеквадратическое отклонение, то соответствую­щая зависимая переменная увеличится или уменьшится на долю среднеквадратического отклонения. Сопоставление бета-коэффициентов позволяет сделать вывод о сравнительной степени воздействия каждо­го фактора на величину результативного показателя.

По аналогии можно сопоставить и коэффициенты эластичности, ко­торые рассчитываются по следующей формуле:

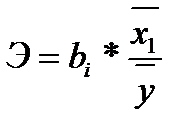
Коэффициенты эластичности показывают, на сколько процентов с среднем изменяется функция с изменением аргумента на 1 %.

5 этап. Статистическая оценка надежности показателей свя­зи для определения надежности уравнения связи и возможности его ис­пользования в практической деятельности с использованием критерия Фишера, критерия Дарбина - Уотсона, средней ошибки аппроксимации, коэффициентов множественной корреляции и детерминации.

Проверенное по всем параметрам уравнение регрессии можно ис­пользовать в практической деятельности для:

1) оценки результатов хозяйственной деятельности предприятия;

2) расчета влияния факторов на изменение результативного пока­зателя;

3) подсчета величины резервов повышения уровня анализируемых показателей.