Использование парной корреляции для изучения стохастических взаимосвязей и правила отбора факторов

Для изучения связи факторного и результативного показателей ис­пользуется парная корреляция.

Для определения влияния фактора на величину результативного показателя с помощью парной корреляции сначала подбирается со­ответствующий тип математического уравнения, которое наилучшим образом отражает характер изучаемой связи (прямолинейный, криво­линейный и т. д.). Это играет важную роль в корреляционном анали­зе, потому что от правильного выбора уравнения регрессии зависят ход решения задачи и результаты расчетов. Обоснование уравнения связи производится с помощью сопоставления параллельных рядов, группировки данных и линейных графиков.

Наиболее простым уравнением, которое характеризует прямоли­нейную зависимость между двумя показателями, является уравнение прямой:

у_х=а+b∙х,

где у_х - результативный показатель;

а,b- параметры уравнения регрессии;

х - факторный показатель.

Это уравнение описывает такую связь между двумя признаками, при которой с изменением факторного показателя на определенную величину наблюдается равномерное возрастание или убывание зна­чений результативного показателя. Коэффициент а - постоянная ве­личина результативного показателя, которая не связана с изменением данного фактора. Параметр b показывает среднее изменение резуль­тативного показателя с повышением или понижением величины фак­тора на единицу его измерения.

Значения коэффициентов а и b находят из системы уравнений, полученных по способу наименьших квадратов. В данном случае сис­тема уравнений имеет следующий вид:

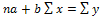
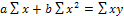
где п - количество наблюдений.

Количество наблюдений при прямолинейной зависимости долж­но составлять не менее двадцати.

Кроме прямолинейной зависимости между изучаемыми показате­лями может возникать и криволинейная зависимость. Если при увели­чении одного показателя значение другого возрастает до определенного уровня, а потом начинает снижаться (например, зависимость произво­дительности труда рабочих от их возраста), то для записи криволиней­ной зависимости лучше всего подходит парабола второго порядка:

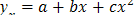
В соответствии с требованиями способа наименьших квадратов для определения параметров а, b и с необходимо решить следую­щую систему уравнений:

.

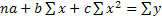
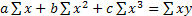
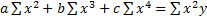Параметры а, b и с находят способом определителей или спосо­бом исключения.

Часто в анализе для записи криволинейных зависимостей ис­пользуется гипербола:

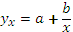
Гипербола описывает такую зависимость между исследуемыми показателями, когда при увеличении одной переменной значения другой увеличиваются до определенного уровня, а потом прирост снижается (например, зависимость себестоимости продукции от объ­ема производства).

Для определения параметров а и b необходимо решить следую­щую систему уравнений:

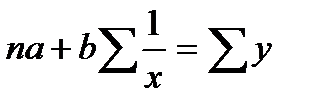
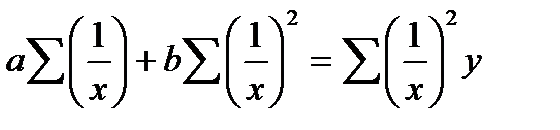
При более сложном характере зависимости между изучаемыми явлениями используются более сложные параболы (третьего, четвер­того порядка и т. д.), а также квадратические, степенные, показатель­ные и другие функции.

Выбор конкретного уравнения регрессии, адекватно описывающе­го форму связи, является довольно сложной процедурой. В условиях использования ПЭВМ выбор адекватной модели в анализе парной корреляции осуществляется перебором решений. Если форму связи сразу установить сложно, решают уравнения нескольких типов. Выбор адекватной модели производится на основе ошибки аппроксимации, которая не должна превышать 0,2, или 20 %. При этом наименьшее значение ошибки аппроксимации свидетельствует о том, что оцени­ваемая модель дает наиболее адекватное описание формы взаимосвязи.

Таким образом, используя определенный тип математического уравнения, можно установить степень зависимости между изучаемыми показателями, т. е. узнать, на сколько единиц в абсолютном измерении изменяется величина результативного показателя с изменением фактор­ного на единицу. Однако регрессионный анализ не позволяет опреде­лить, является ли тесной полученная связь и оказывает ли решающее воздействие данный фактор на величину результативного показателя.

Для измерения тесноты связи между факторными и результа­тивным показателями определяется:

- при прямой зависимости - коэффициент корреляции:

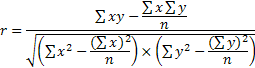
- при криволинейной зависимости - корреляционное отношение:

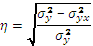
где 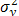- общая дисперсия, рассчитываемая по формуле:

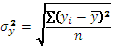
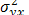- межгрупповая дисперсия, определяемая формулой:

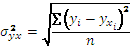
Коэффициент корреляции (корреляционное отношение) прини­мает значение от 0 до 1 и характеризирует вид связи между результа­тивным и факторным показателями:

если 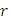( 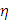) = 0, то связь отсутствует;

если 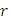( 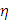) = 1, то связь функциональная (детерминированная);

если 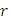( 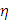) - отрицательная величина, то связь между показате­лями обратная.

Коэффициент корреляции (корреляционное отношение) дает количественную оценку тесноты связи, характеризирует силу влия­ния факторного показателя на изменение результативного. Теснота связи в зависимости от значения величины коэффициента корреля­ции (корреляционного отношения) подразделяется следующим об­разом:

- слабая, если величина коэффициента корреляции (корреляцион­ного отношения) от 0,3 до 0,5;

- умеренная, если величина коэффициента корреляции (корреля­ционного отношения) от 0,5 до 0,7;

- заметная, если величина коэффициента корреляции (корреля­ционного отношения) от 0,5 до 0,7;

- высокая, если величина коэффициента корреляции (корреляци­онного отношения) от 0,7 до 0,9;

- весьма высокая, если величина коэффициента корреляции (кор­реляционного отношения) от 0,9 до 0,99.

Если коэффициент корреляции возвести в квадрат, то получим коэффициент детерминации, отражающий долю влияния иссле­дуемого фактора на результативный показатель.

При значениях тесноты связи меньше 0,7 величина коэффици­ента детерминации факторного признака всегда меньше 50 %. Это означает, что на долю вариации факторного признака x_i приходится меньшая доля по сравнению с другими признаками, влияющими на изменение результативного показателя. Синтезированные при та­ких условиях математические модели связи практического значе­ния не имеют. Поэтому использование корреляционного и регрес­сионного анализа эффективно в первую очередь для определения взаимозависимости между результативным и факторным показате­лями при линейной зависимости.