Моделирование на метауровне

Математические модели на микроуровне учитывали распределенностью параметров объекта в пространстве. Переход на макроуровень характеризуется дискретизацией пространства – параметры объекта считаются сосредоточенными в отдельных точках пространства. Метауровень имеет математические модели, где вводятся еще большие допущения и упрощения, что позволяет получать доступные для исследования математические модели больших объектов и систем.

Существует несколько способов построения математических моделей на метауровне, к ним относятся:

1) дискретизация времени, т. е. наряду с введением сосредоточенных параметров переменные и параметры модели считаются независящими непрерывно от времени;

2) потери энергии в объекте не учитываются;

3) переход к факторным моделям;

4) переход к функциональным моделям, в которых используется только один вид фазовой переменной – сигнал;

5) эквивалентирование – замена больших систем их упрощенными моделями – эквивалентами, созданными на основе специальных критериев, и др.

Так, например, решать задачи регулирования частоты и обменной мощности в Единой энергосистеме (ЕЭС) России можно с помощью модели, которая может обозримо представить все составные части этого большого и сложного объекта с учетом пропускной способности межу объединениями энергосистем (ОЭС). На рис. 1.6 показаны связи между отдельными ОЭС, входящими в ЕЭС России. Параметрами такой модели могут служить значения пропускной способности связей, мощности отдельных ОЭС и «коэффициенты жесткости» (отношения предела статической устойчивости связи к меньшей мощности из соединяемых частей ОЭС). В такой модели параметры и переменные могут считаться неизменными на длительных интервалах времени и потери электрической энергии не учитываются.

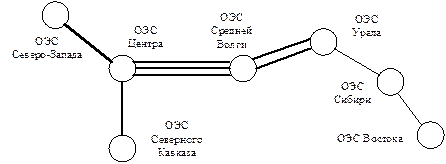
Рис 1.6. Схема связей между ОЭС ЕЭС России

Переход к факторным моделям может быть выполнен методами идентификации объектов или с использованием методов планирования эксперимента. Идентификация технических объектов рассматривается в разделе 4.

Функциональное моделирование является предметом изучения отдельной дисциплины – теории автоматического регулирования.

Эквивалентирование – это преобразование электрической схемы на основе специальных критериев с целью ее упрощения. Обычно в сложной ЭЭС выделяется часть схемы сети, для которой выполняется анализ режимов работы, все остальные преобразуются в эквивалентные схемы. Так, рассматривая режимы работы отдельной ЭЭС, все соседние энергосистемы представляют их эквивалентами или в большом энергообъединении сохраняются только мощные высоковольтные линии и подстанции, а сети более низкого напряжения представляются эквивалентами.

Вопросы для самопроверки

1. Какое свойство модели является фундаментальным?

2. Как классифицируются модели?

3. По каким признакам различают переменные в математических моделях?

4. Чем различаются прямые и обратные задачи исследования объекта при его моделировании?

5. Как подразделяются дискретные переменные в математических моделях?

6. Поясните свойство адекватности математической модели.

7. Назовите попарно противоположные свойства объектов с точки зрения моделирования.

8. Что представляют собой математические модели на микро-уровне?

9. Что представляют собой математические модели на макро-уровне?

10. Что представляют собой математические модели на метауровне?

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ
ЭЛЕМЕНТОВ ЭЭС