Линия электропередачи
2.1.1. Конструктивное выполнение и свойства
линии электропередачи
В простейшем представлении линия электропередачи – это проводники, протянутые на большое расстояние, по которым передается электрическая энергия. Возможность передачи электроэнергии обусловлена главным образом большим напряжением, при котором потери при передаче снижаются до приемлемого уровня.
Конструктивно воздушные ЛЭП представляет собой провода, подвешенные на безопасном расстоянии от земли, или кабели, в которых проводящие жилы изолированы друг от друга и от внешней среды и защищены различными покровами и броней. В зависимости от конструкции ЛЭП называют воздушными (ВЛ) или кабельными линиями (КЛ).
Практически во всем мире для передачи электрической энергии принята система трехфазного переменного тока 50 или 60 Гц. Однако
в некоторых случаях применяются другие системы переменного тока и передачи постоянного тока. Будем рассматривать только трехфаз-ные воздушные линии переменного тока высокого напряжения (до 1150 кВ), передающие электроэнергию на большие расстояния (до нескольких тысяч километров).
Передача электроэнергии по ЛЭП переменного тока обусловлена распространением электромагнитного поля в проводах и окружающем пространстве. Возникновение переменного электростатического поля приводит к появлению токов смещения – зарядных токов (рис. 2.1). Зарядные токи, накладываясь на нагрузочный ток, определяют постепенное изменение тока вдоль линии. Магнитное поле, обусловленное током линии, характеризуется напряженностью, также изменяющейся вдоль линии. Это приводит к наведению ЭДС самоиндукции и взаимоиндукции, неравных для различных участков линии. Неравенство этих ЭДС определяет сложный закон изменения напряжения вдоль линии, в свою очередь определяющий изменение токов смещения вдоль линии.

Рис. 2.1. Условное изображение распределения токов вдоль провода ЛЭП
В общем случае ЛЭП следует рассматривать как объект с распределенными вдоль одной пространственной координаты параметрами (вдоль линии). Параметры линии электропередачи, к которым относятся активное сопротивление, индуктивность, активная проводимость и емкость на единицу длины, считают равномерно распределенными вдоль ее длины. Такое свойство линий называют однородностью.
Провода ВЛ имеют в качестве проводящего материала алюминий или его сплав. Практически всегда используются сталеалюминиевые провода марки АС. Их удельное сопротивление постоянному току в среднем равно r = 29,1 Ом мм2 / км. Активное сопротивление переменному току больше сопротивления постоянному току вследствие поверхностного эффекта, однако для частоты 50 Гц это различие несущественно. Активное сопротивление в электрических схемах ЛЭП является параметром, определяющим процесс диссипации (рассеивания) энергии в виде отдачи тепла в окружающее пространство.
Индуктивность ЛЭП вызвана явлениями самоиндукции и взаимоиндукции фаз линии и определяется в зависимости от диаметра проводов фазы и расстояния между фазами. В практике расчетов электрических сетей используют индуктивное сопротивление фаз ЛЭП. Погонное индуктивное сопротивление ВЛ 330–1150 кВ x0 в среднем равно 0,31 Ом / км.
Вследствие несовершенства изоляции ВЛ и явления короны в местах присоединения проводов к гирляндам изоляторов ВЛ имеют место потери электроэнергии от токов утечки по изоляторам ВЛ и короны. Большое влияние на эти потери оказывают влажность и загрязнение окружающего воздуха. В зависимости от погоды потери от токов утечки и на корону могут изменяться в десятки раз.
Моделирование потерь в изоляции ВЛ можно выполнить с помощью введения активной проводимости g0, величина которой определяется по экспериментальным данным, полученным в результате наблюдений и расчетов существующих ВЛ. Для большинства ВЛ 330–1150 кВ погонная активная проводимость задается в пределах 0,01…0,1 мкСм / км.
Емкостные проводимости между фазами и между проводами и землей, грозозащитными тросами и заземленными частями опоры моделируются одним параметром – емкостной проводимостью фазы b0. Величина погонной емкостной проводимости ВЛ 330–1150 кВ в среднем составляет 3,5 мкСм / км.
В цепи с распределенными параметрами интервал времени распространения электромагнитных волн вдоль линии сопоставим с интервалом времени, в течение которого токи и напряжения изменяются на заметную величину от полного их изменения.
Другими свойствами линии электропередачи можно считать:
· непрерывность переменных;
· стационарность;
· одномерность в отношении пространства и многомерность в отношении переменных, характеризующих работы линии в разных точках линии;
· статизм или динамичность (в зависимости от исследуемых процессов);
· линейность или нелинейность (в зависимости от уравнений, описывающих режим работы линии) – при этом параметры линии считаются постоянными величинами.
В отношении детерминированности и стохастичности рассматриваются разные подходы к моделированию линии – параметры и переменные могут быть представлены также и случайными величинами.
2.1.2. Математическая модель линии
с распределенными параметрами
Элементы ЭЭС являются, как правило, трехфазными устройствами переменного тока, и ЛЭП имеет три фазы, которые присоединяются к другим трехфазным элементам сети, например, повышающим и понижающим трансформаторам (рис. 2.2, а).
Здесь и далее будем рассматривать только симметричные трехфазные системы, которые вследствие симметрии можно графически изображать в однолинейном виде (рис. 2.2, б), имея в виду, что протекающий по фазе переменный ток замыкается через две другие фазы. Кроме того, трехфазная система имеет нейтраль N, которая технически может отсутствовать, но токи утечки и емкостные токи в линии могут моделироваться посредством введения нейтральной точки (линии, плоскости). На рис. 2.2 соединение обмоток трансформаторов в звезду дает нейтральные точки трехфазной системы, которые могут иметь соединение с землей (заземление).
Выделим в линии на расстоянии x от начала линии (рис. 2.2, а, точка 1) участок бесконечно малой длины dx. На этом участке линии электрические параметры можно считать сосредоточенными (рис. 2.3).
|
|

Рис. 2.2. Трехфазная линия электропередачи (а) и ее однолинейное изобра-
жение (б)
Составим уравнения Кирхгофа для электрической цепи на выделенном участке линии:
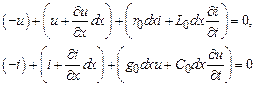
или
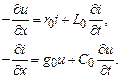
Здесь в C0 и L0 учтены влияния соседних фаз линии.
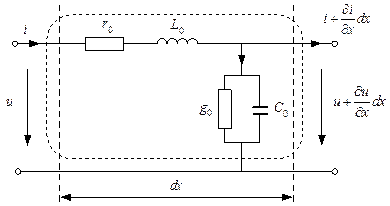
Рис. 2.3. Элементарный отрезок линии
Полученные уравнения являются дифференциальными уравнениями в частных производных – моделью участка линии на микроуровне. Независимые переменные в них – это время t и одна пространственная координата x.
Используя символический метод представления синусоидальных функций времени комплексными величинами, для действующих значений токов и напряжений можно записать:
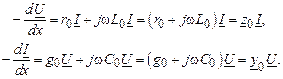
Полученная система уравнений уже имеет одну независимую переменную x. Обозначим напряжения и токи по концам линии: U1 и I1 при x = 0 и U2 и I2 при x = l. Тогда из решения системы дифференциальных уравнений (2.3) получим связь между напряжениями и токами по концам линии:
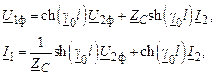
где 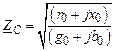 – волновое сопротивление линии;
– волновое сопротивление линии;
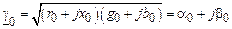 – коэффициент распространения волны;
– коэффициент распространения волны;
α0 – коэффициент затухания волны;
β0 – коэффициент фазы.
Полученные уравнения называются уравнениями длинной линии или телеграфными уравнениями.
В (2.4) напряжения записаны в фазных значениях. Однако в трехфазных системах принято указывать линейные значения напряжений, что приводит к пересчету на  некоторых слагаемых:
некоторых слагаемых:
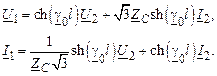
Чтобы не вводить в запись уравнений константу 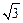 и в то же время использовать линейные значения напряжений, используют увеличенное в
и в то же время использовать линейные значения напряжений, используют увеличенное в 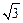 значение тока линии. Таким образом, математическая модель длинной линии имеет вид
значение тока линии. Таким образом, математическая модель длинной линии имеет вид
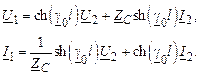
Здесь I1 и I2 – фазные токи линии, увеличенные в 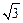 .
.
Когда необходимо вычислить напряжение и ток в какой-либо другой точке линии, находящейся на расстоянии x от начала линии (рис. 2.4), по напряжению и току в конце, используют модель:
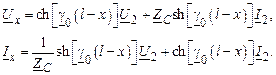
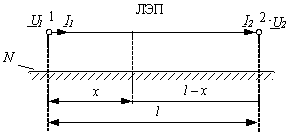
Рис. 2.4. Определение напряжения и тока в точке
на линии
Формально напряжение и ток в любой точке линии можно рассматривать как результат наложения двух волн, движущихся в противоположные стороны. С течением времени волна напряжения перемещается от начала линии к ее концу; она носит название прямой или падающей волны. Волна напряжения, которая перемещается от конца линии к ее началу, носит название обратной или отраженной волны.
Расчеты показывают, что для воздушных линий электропередачи при частоте f = 50 Гц коэффициент фазы β0 ≈ 0,001 рад/км (0,06 град/км). С помощью этого значения можно найти длину прямой и обратной волн.
Введем понятие длины волны напряжения и тока λ, равной расстоянию между двумя точками линии, в которых фазы напряжения (тока) падающей или отраженной волны напряжения (тока) различаются на 2π.
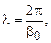
где 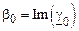 – коэффициент фазы.
– коэффициент фазы.
Скорость перемещения падающей волны вдоль линии называется фазовой скоростью волны. Это скорость перемещения точки, фаза колебания в которой остается постоянной:
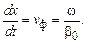
Из этого соотношения с учетом ω = 2πf получим более точное значение коэффициента фазы
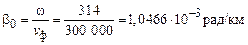
и длины волны
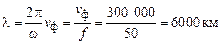 .
.
Линии с длиной l = λ = 6000 км называют волновыми, а с l = λ / 2 =
= 3000 км – полуволновыми линиями.
Для упрощения исследований режимов работы ЛЭП сверхвысокого напряжения иногда пользуются уравнениями идеальной линии, в которой активные параметры считаются равными нулю: r0 = 0, g0 = 0. Очевидно, что при этом α0 = 0.
С учетом
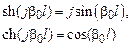
получим математическую модель идеальной линии:
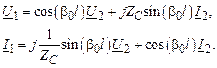
2.1.3. Математические модели линии
в виде схем замещения
Систему уравнений (2.6) можно представить как уравнения четырехполюсника (рис. 2.5).
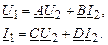

Рис. 2.5. Четырехполюсник
Здесь 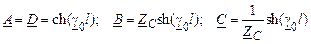 , что позволяет считать данный четырехполюсник симметричным.
, что позволяет считать данный четырехполюсник симметричным.
В практике расчетов удобно пользоваться П-образной схемой замещения линии (рис. 2.6).
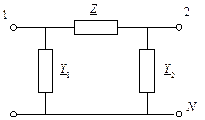
Рис. 2.6. П-образная схема заме-
щения ЛЭП
Найдем соотношения, связывающие параметры П-образной схемы замещения Z, Y1 и Y2 с параметрами модели длинной линии (2.6).
Запишем выражение, связывающее напряжения в начале U1 и конце U2 П-образной схемы замещения:
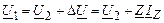 ,
,
где ΔU – падение напряжения в продольной ветви на параметре Z схемы замещения;
IZ – ток в ветви с параметром Z.
Соотношения между токами в ветвях схемы замещения получаются из первого закона Кирхгофа:
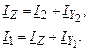
Токи в поперечных ветвях с Y1 и Y2 вычисляются по формулам:
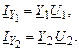
Подставим ток IZ из (2.16) в (2.15) и с учетом (2.17) будем иметь:
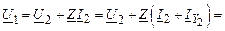
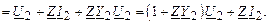
Теперь запишем соотношение для тока в начале схемы замещения I1, выразив его также через напряжение и ток конца схемы замещения. Подставив в выражение для тока I1 из (2.16) выражения для тока IZ и тока IY1, получим
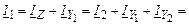
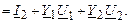
Подставим в это выражение U1 из (2.18), будем иметь:
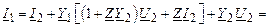
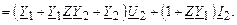
Окончательно получаем систему уравнений для П-образной схемы замещения:
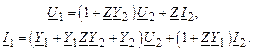
Модель (2.21) по своей структуре совпадает с уравнениями четырехполюсника (2.14). Из этого с учетом вида модели длинной линии (2.6) следует, что
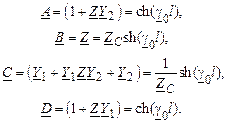
Решение (2.22) относительно параметров П-образной схемы замещения дает:
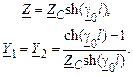
Используя известные математические соотношения
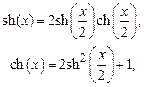
получаем
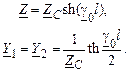
Для идеальной линии параметры П-образной схемы замещения получаются в виде
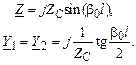
Пример 1. Найдем распределение величины напряжения и тока вдоль ЛЭП 500 кВ длиной L = 500 км при холостом ходе и при передаче мощности нагрузки меньше и больше натуральной мощности линии. Конструкция фазы линии: 3хАС-400/51. Расчеты и графические построения выполним в системе Mathcad. Приведенные ниже значения параметров линии выражены в омах, сименсах и радианах. Параметры режима ЛЭП даны в киловольтах, килоамперах, мегаваттах и мегаварах.
Длина и погонные параметры линии:
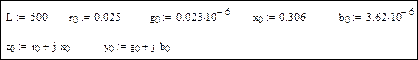
Расчетные параметры линии – волновое сопротивление, коэффициент распространения волны и натуральная мощность:
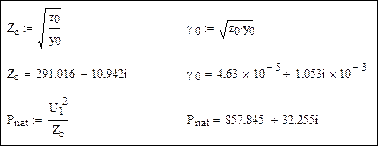
Дата добавления: 2015-03-19; просмотров: 11410;
