Детерминированное моделирование и требования предъявляемые к нему. Типы факторных детерминированных моделей

Одной из задач факторного анализа является моделирование взаимосвязей между результативным и факторными показателями. Сущность моделирования заключается в том, что взаимосвязь иссле­дуемого показателя с факторами представляется в форме конкретного математического уравнения и может быть функциональной или кор­реляционной.

С помощью детерминированных факторных моделей исследуют­ся функциональные взаимосвязи между показателями. При этом при построении факторной модели должны соблюдаться следующие требования:

1) факторы, включаемые в модель, должны реально существо­вать, а не являться абстрактными величинами;

2) факторы должны находиться в причинно-следственной взаи­мосвязи с исследуемым результативным показателем;

3) все показатели факторной модели должны быть количественно измеримы, иметь единицу измерениями необходимую информацион­ную обеспеченность;

4) факторная модель должна обеспечивать возможность измере­ния влияния отдельных факторов;

5) вначале в факторную модель записываются количественные факторы, затем качественные;

6) если в факторной модели присутствует несколько количест­венных или качественных факторов, то вначале записываются факто­ры более высокого порядка, а затем факторы более низкого порядка.

В детерминированном факторном анализе можно выделить сле­дующие типы факторных моделей.

1. Аддитивные модели используются в том случае, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей:

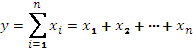
2. Мультипликативные модели применяются в том случае, когда результативный показатель представляет собой произведение нескольких факторных показателей:

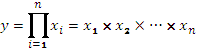
3. Кратные модели применяются в том случае, когда результативный показатель определяется отношением величины одного факторного показателя к величине другого:

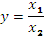
4. Смешанные (комбинированные) модели представляют собой сочетание в различных комбинациях предыдущих моделей, например:

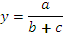
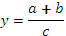
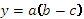
Построенная факторная модель для проведения более глубокого анализа может подвергаться дальнейшему преобразованию. С этой целью используется ряд способов и приемов. При этом от того, на­сколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа хозяйственной деятельности предприятия.

Моделирование аддитивных факторных систем осуществля­ется путем последовательного разложения факторов исходной фак­торной системы на составные элементы:

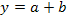
Факторы первого уровня а и b зависят, в свою очередь, от ряда других факторов:

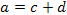
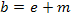
Тогда

у = с+d+е+т

Моделирование мультипликативных факторных систем представляет собой процесс детализации путем последовательного разложения комплексных факторов исходной факторной системы на факторы-сомножители:

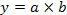
Факторы первого уровня а и b зависят, в свою очередь, от ряда других факторов:

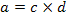
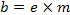
Тогда

у = с∙d∙е∙т

При моделировании кратных моделей применяют следующие способы их преобразования:

1) способ удлинения, предусматривающий преобразование чис­лителя исходной факторной модели путем замены одного или не­скольких факторов на сумму однородных показателей:

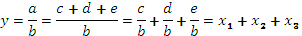
2) способ формального разложения предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных пока­зателей:

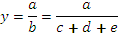
3) способ расширения предусматривает преобразование исход­ной факторной модели путем умножения числителя и знаменателя дроби на один или несколько новых показателей:

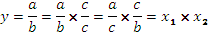
4) способ сокращения представляет создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель:

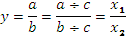
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных факторных моделей. Выбор способа моделирования зависит от объекта исследования и от поставлен­ных целей, а также от профессиональных знаний и навыков исследователя.

Вопросы для самоконтроля:

1. Что понимается под факторным анализом?

2. Какие основные задачи факторного анализа?

3. В чем суть детерминированного и стохастического факторного анализа?

4. В чем суть прямого и обратного факторного анализа и какой из них имеет большее значение?

5. В чем суть ретроспективного и перспективного факторного анализа?

6. Каковы основные признаки классификации факторов в анали­зе хозяйственной деятельности?

7. Какие основные типы факторных моделей применяются в де­терминированном анализе?

8. Как производится преобразование факторных моделей методом расширения, удлинения и сокращения?