Решение. 1) Рассмотрим равновесие конструкции, состоящей из двух плит (рис
1) Рассмотрим равновесие конструкции, состоящей из двух плит (рис. 5.15).
2) На плиту действуют заданные силы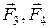 
, пара сил с моментом М, вес обеих плит.
3) Связи: А – сферический шарнир, В – цилиндрический шарнир (подшипник), 1 – стержень. Реакцию сферического шарнира А разложим на три составляющие {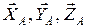 
}, цилиндрического (подшипника) – на две составляющие { 
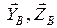} (в плоскости, перпендикулярной оси подшипника); реакцию 
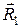стержня 1 направим вдоль стержня 1 (считаем, что он сжат).
4) Для определения шести неизвестных реакций {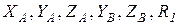 
} составим шесть уравнений равновесия действующей на плиту пространственной системы сил:
;
;
;
; 
;
; 
;
; 
.
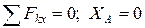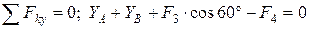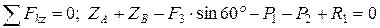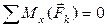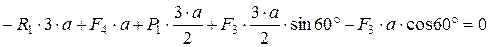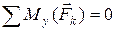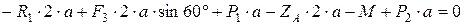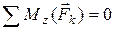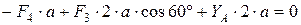5) Подставим числовые значения всех заданных величин и, решив полученную систему уравнений, найдем искомые реакции:
R1 = 9,1 кН; XA = 0 кН; YA = 1 кН; ZA = 0,225 кН; YB = 6 кН; ZB = 7,335 кН.
Пример 3. На вертикальный вал (рис. 5.16) действуют две силы: F1 = 10 кН; F2 = 4 кН; равномерно распределенная нагрузка интенсивностью q = 2 кН/м; пара сил с моментом М. Под действием заданных силовых факторов вал находится в покое. Тело 2, весом F1, находится на гладкой наклонной поверхности.
Определить реакции в цилиндрическом подшипнике А и упорном подшипнике В, если а=1м и a = 60°.
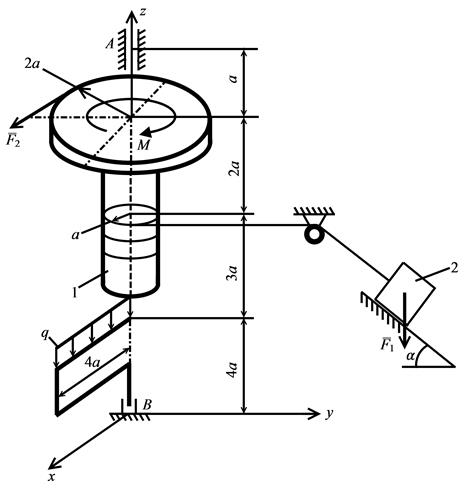
Рис. 5.16
Решение.
Несвободную пространственную конструкцию вал 1 можно представить формально свободной, если мысленно отбросить связи и их действие на вал заменить реакциями связей.
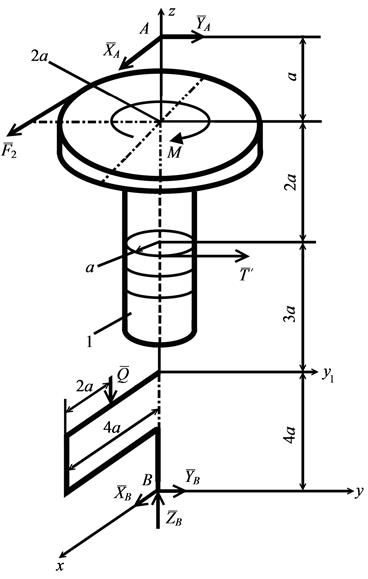
Расчетные схемы представлены на рис. 5.17, 5.18.
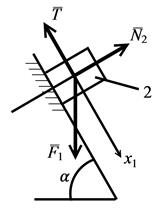
Для определения усилия Т в нити рассмотрим отдельно равновесие тела 2 (рис. 5.18).
 
| |
| Рис. 5.17 | Рис. 5.18 |
Применяя одно уравнение статики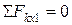 
, 
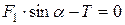, находим:
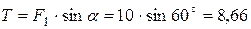кН.
Для системы сил, действующих на вал, запишем шесть уравнений:
; 
;
; 
;
; 
;
; 
;
; 
;
; 
.
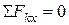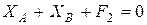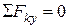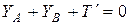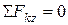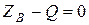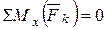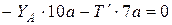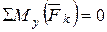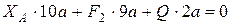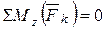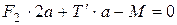При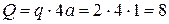 
кН из пятого уравнения находим 
:
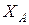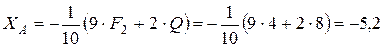кН.
Шестое уравнение, при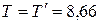 
кН, определяет момент пары сил:
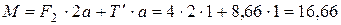кН×м.
Из четвертого уравнения находим:
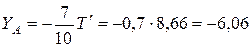кН.
Из первых двух уравнений находим:
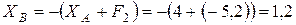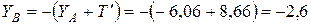кН;
кН.
Наконец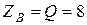 
кН.
Ответ: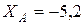 
кН; 
кН;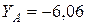 
кН; 
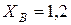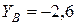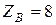кН; 
кН;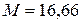 
кН×м.
Проверка. Вычислим сумму моментов всех сил относительно оси у1:
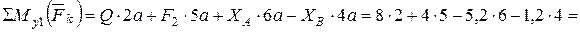
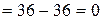
Все реакции найдены верно.
Дата добавления: 2015-03-17; просмотров: 1623;