Пример выполнения расчетно-графической работы по теме. «Определение реакций опор пространственной конструкции»

«Определение реакций опор пространственной конструкции»

Пример 1. Однородная прямоугольная пластинка весом Р = 60Н прикреплена к стене при помощи шарового шарнира А и цилиндрического шарнира В. Пластинка удерживается в горизонтальном положении тросом СЕ, наклоненному к горизонтальной плоскости под углом 30°. Определить натяжение троса и опорные реакции.

Решение.

1) Рассмотрим равновесие пластинки АВСD, т.е. объектом исследовании задачи является данная пластинка (рис. 5.14).

2) Приложим к пластинке заданную силу тяжести в точке пересечения диагоналей пластинки;

3) Освободим тело от наложенных на него связей (в точке А – шаровой шарнир, в точке B – цилиндрический шарнир и в точке C – нить). Реакцию шарового шарнира разложим на три составл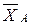яющие { , , }, цилиндрического шарнира – на две составляющие { , } (в плоскости, перпендикулярной оси цилиндрического шарнира); реакцию нити 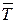направим вдоль нити от точки C к точке E.

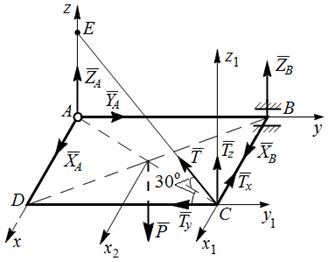
Рис.5.14

4) Для определения величин шести неизвестных реакций связей { 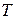, , 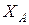, , 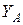, } составим 6 уравнений равновесия действующей на пластинку произвольной пространственной системы сил. Переходя к составлению уравнений равновесия, заметим, что неизвестны углы, которые образует сила 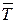с осями x и y, поэтому разложим силу 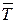на две составляющие, чтобы одна из них, , лежала в плоскости xy пластинки, а вторая, 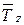, была параллельна оси z, т.е. 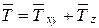. Модули этих составляющих равны: 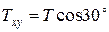; 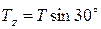. Затем составляющую разложим по осям координат x и y: , .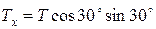

Составим уравнения равновесия данной системы:

∑ Fkx = 0;	XA + XB – Tx = 0;	(1)
∑ Fky = 0;	YA – Ty = 0;	(2)
∑ Fkz = 0;	ZA + ZB – P + Tz = 0;	(3)
∑ mx( k) = 0;	ZВ·AB – P·AB/2 + Tz·AB = 0;	(4)
∑ my( k) = 0;	P·ВC/2 - Tz·ВC = 0;	(5)
∑ mz( k) = 0;	-XB·AB = 0.	(6)

Из уравнения (6): X_B = 0.

Из уравнения (5): T_Z = Р/2=60/2 = 30Н.

Отсюда: T = T_z/sin30° = 30/0,5 = 60Н; T_x = 25,98Н; T_y = 45Н.

Из уравнения (1): X_A = T_x - X_B = 25,98Н.

Из уравнения (2): Y_A = T_y = 45Н.

Из уравнения (4): Z_В = P/2 - T_z = 30 -30 = 0.

Из уравнения (3): Z_A = P - T_z - Z_B = 60-30-0 = 30Н.

Проверка:

Уравнение моментов относительно оси x₁:

∑mx1( k) = 0; -30 + 0 + 30 = 0;

-ZА·AB/2 + ZВ·AB/2 + Tz·AB/2 = 0; 0 = 0.

Уравнение моментов относительно оси y₁:

∑my1( k) = 0; (30 + 0) – 60/2 = 0;

(ZА+ZВ) ·BC – P·BC/2 = 0; 0 = 0.

Уравнение моментов относительно оси z₁:

∑mz1( k) = 0; 25,98·AB – 45·AB· = 0;

XА·AB - YA·BC = 0; 0 = 0.

Проверка сошлась.

Ответ: X_B = 0Н; Z_В = 0Н; T = 60Н; X_A = 25,98Н; Y_A = 45Н; Z_A = 30Н.

Пример 2. Две однородные прямоугольные плиты жестко соединены под прямым углом друг к другу и закреплены сферическим шарниром в точке A, цилиндрическим шарниром в точке B, а также невесомым стержнем 1 (рис. 5.15). Размеры плит указаны на рисунке. Определить реакции связей, если известно, что веса плит равны Р₁=5кН; Р₂=3кН; момент пары сил равен М=4 кН м; а=0,6 м; модули заданных сил F₃=10 кН; F₄=12 кН; ₃=60°, силы приложены к серединам стороны плиты.

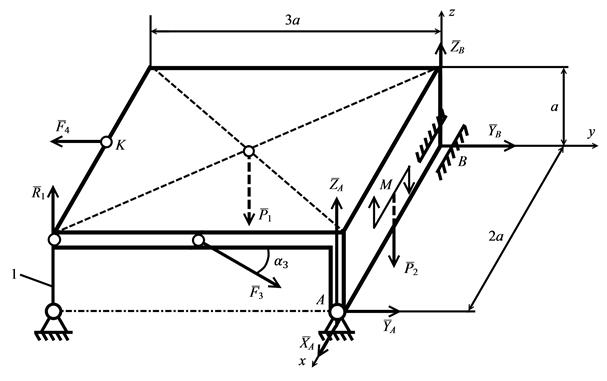
Рис. 5.15