По исследованию условий равновесия произвольной плоской системы сил, приложенной к твердому телу
При практическом решении задач можно пользоваться любой формой уравнений равновесия, так как все они совершенно равноправны. Изложим некоторые общие правила составления уравнений равновесия.
Оси координат и моментные точки можно выбирать произвольно. Наиболее просто и безошибочно решаются уравнения равновесия, в которые входит одно неизвестное. Следовательно, координатные оси надо направлять перпендикулярно к направлению неизвестных сил. Тогда при составлении уравнений проекций неизвестные, перпендикулярные к осям, в эти уравнения не войдут. За моментные целесообразно брать такие точки, в которых пересекаются линии действия двух неизвестных сил. Тогда в уравнение моментов войдет только одна искомая сила.
Для плоской системы можно выбирать любое число координатных осей и моментных точек и составлять соответствующее число уравнений равновесия, но только три из них будут независимыми. Остальные уравнения получаются как следствия из этих трех и их можно использовать лишь для проверки.
Для плоской системы параллельных сил эти общие правила можно конкретизировать. Оси координат следует направлять так, чтобы одна из них оказалась параллельной силам, приложенным к твердому телу. Уравнение моментов нужно составлять относительно точки, лежащей на линии действия неизвестной силы. Это дает возможность определить одну из неизвестных сил непосредственно из одного уравнения моментов. Для решения задач при помощи двух уравнений моментов следует учитывать, что моментные точки не должны лежать на прямой, параллельной силам.
Задачи на равновесие твердого тела для плоской системы сил рекомендуется решать в следующем порядке:
1. Выделить тело, равновесие которого надо рассмотреть.
2. Изобразить активные (заданные) силы.
Освободить тело от связей, приложив соответствующие реакции. При этом необходимо убедиться, что данная задача является статически определимой – число неизвестных величин должно быть не более трех (для системы параллельных сил – не более двух).
3. Направить оси координат и выбрать моментные точки.
4. Составить уравнения равновесия произвольной плоской системы сил (или плоской системы параллельных сил).
5. Решить систему полученных уравнений равновесия относительно неизвестных величин.
Если в результате решения искомая реакция получается положительной, то это значит, что направление ее выбрано верно, если отрицательной, то направление реакции противоположно выбранному (модуль ее при этом остается прежним).
После того как задача решена, необходимо произвести проверку. Для этого следует составить не применявшуюся при решении сумму моментов или проекций, при этом необходимо учитывать уже исправленные направления реакций. Равенство нулю алгебраической суммы проекций или моментов подтвердит правильность решения задачи.
Пример решения задачи с использованием первой (основной) формы
уравнений равновесия
Пример. Горизонтальная балка длиной 5 м заделана в стену (рис. 2.21). На балку действует равномерно распределенная нагрузка интенсивностью q=1,5 Н/м на участке длиной 3 м, а также пара сил с моментом 2 Н·м и сила F = 4Н.
Определить реакции заделки: XA, YA, MA.
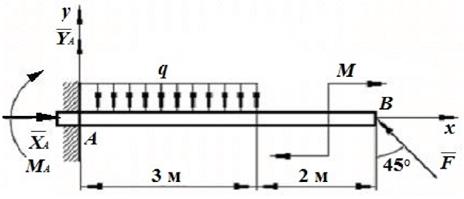 Рис. 2.21
Рис. 2.21
|
Решение: Задача сводится к определению реакции опоры жесткой заделки, при действии на балку равномерно распределенной нагрузки, момента пары сил и силы, приложенной к концу балки под углом 45°.
1. Рассматриваем равновесие плоской системы сил, действующей на балку.
2. Показываем все действующие на балку силы и момент пары сил.
3. Мысленно отбрасываем связи и заменяем их реакциями 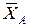 ,
, 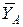 ,
, 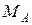 . Направления
. Направления 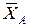 ,
, 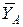 принимаем совпадающими с направлением осей координат Axy.
принимаем совпадающими с направлением осей координат Axy.
4. Составляем три уравнения равновесия:
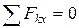 ;
; 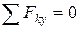 ;
; 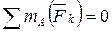 .
.
Из трех уравнений можно определить три неизвестные величины.
Составим уравнения равновесия сил:
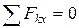 ;
; 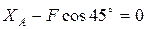 ;
; 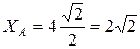 Н;
Н;
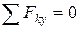 ;
; 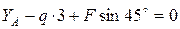 ;
; 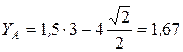 Н;
Н;
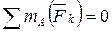 ;
; 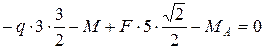 ;
;
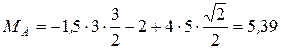 Н∙м.
Н∙м.
Ответ: 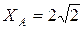 Н;
Н; 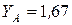 Н;
Н; 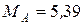 Н∙м.
Н∙м.
Проверка. Сумма моментов относительно точки В:
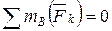 ;
; 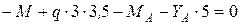 ;
;
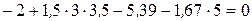 ;
;  .
.
Проверка сошлась.
Пример решения задачи с использованием второй формы
уравнений равновесия
Пример. Однородная балка АВ весом 200 Н и длиной 3 м опирается на гладкий горизонтальный пол в точке В под углом 60° и, кроме того, поддерживается двумя опорами С и D (рис. 2.22), причем СВ= 0,5 м, BD = 1 м.
Определить реакции опор в точках В, С и D: NC, ND, NB.
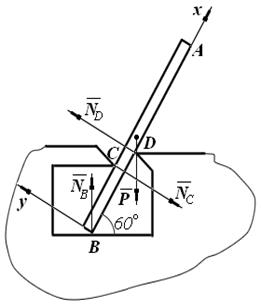
Рис. 2.22
Решение: Задача сводится к определению реакций опор в точках В, С, D при действии на балку силы тяжести Р = 200 Н.
1. Рассмотрим равновесие плоской системы сил, действующей на балку.
2. Приложим посередине балки силу тяжести 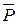 .
.
3. Проведем оси координат через точку B, направив ось x параллельно оси балки.
4. Мысленно отбрасываем связи и заменяем их реакциями 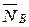 ,
, 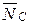 ,
, 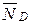 .
.
5. Составляем три уравнения равновесия: 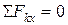 ;
; 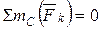 ;
; 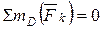 , из которых можно найти три неизвестных величины.
, из которых можно найти три неизвестных величины.
Составим уравнения равновесия сил:
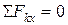 ;
; 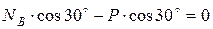 ;
; 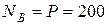 Н;
Н;
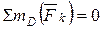 ;
; 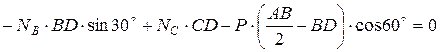 ;
;
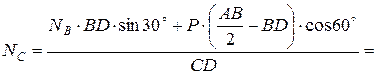
= 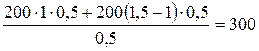 Н;
Н;
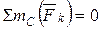 ;
; 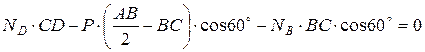 ;
;
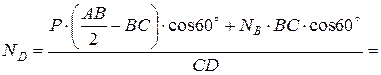
= 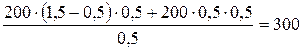 Н.
Н.
Ответ: 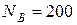 Н;
Н; 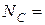
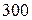 Н;
Н; 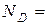
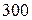 Н.
Н.
Проверка. Сумма моментов относительно точки В:
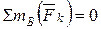 ;
; 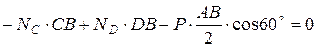 ;
;
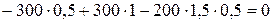 ;
; 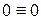 . Проверка сошлась.
. Проверка сошлась.
Пример решения задачи с использованием третьей формы
уравнений равновесия
Пример. Тяжелая балка весом G удерживается в горизонтальном положении тремя тросами (рис. 2.23). Определить натяжения тросов: 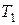 ,
, 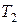 и
и 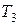 .
.
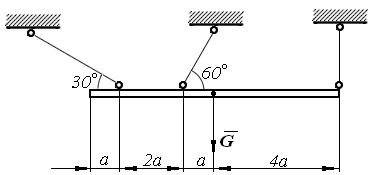
Рис. 2.23
Решение:
1. Рассмотрим равновесие балки.
2. Приложим силу тяжести 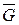 .
.
3. Отбросим связи, заменив их реакциями тросов: 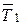 ,
, 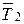 и
и 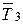 , численно равными искомым натяжениям. Так как число неизвестных равно трем, то задача статически определима.
, численно равными искомым натяжениям. Так как число неизвестных равно трем, то задача статически определима.
4. Выберем три моментные точки А, В и С (рис. 2.24), в каждой из которых пересекаются по две неизвестные силы, и составим три уравнения:
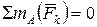 ;
; 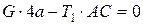 ;
;
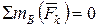 ;
; 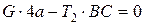 ;
;
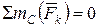 ;
; 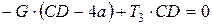 .
.
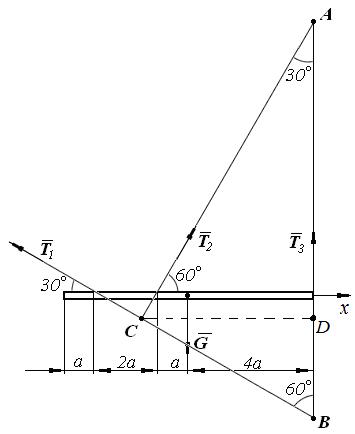
Рис. 2.24
Находим величины АС, ВС и СD:
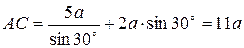 ;
; 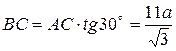 ;
; 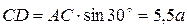 .
.
Тогда, решая полученную систему уравнений, получим, что:
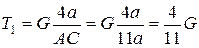 ;
;
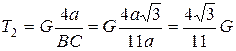 .
.
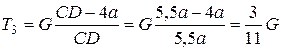 .
.
Ответ: 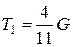 ;
; 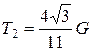 ;
; 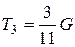 .
.
Проверка. Сумма проекций всех сил на ось Ox:
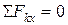 ;
; 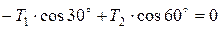 ;
;
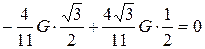 ;
; 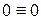 . Проверка сошлась.
. Проверка сошлась.
Дата добавления: 2015-03-17; просмотров: 1573;
