Показатели процесса технической эксплуатации

Функция распределения времени безусловного пребывания процесса в состоянии i

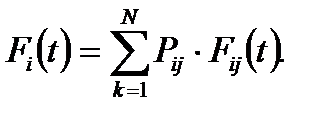(5.1)

Здесь k – номер состояния.

Если µ_ij – среднее время, соответствующее распределению F_ij(t), то из выражения (5.1) можно получить среднее время µ_i безусловного пребывания процесса в состоянии i, т.е.

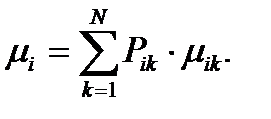
Если обозначить через l_ij среднее время до первого попадания процесса из состояния i в состояние j можно получить

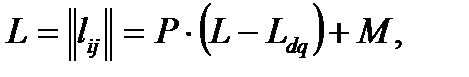(5.2)

где М – матрица, элементами которой служат безусловные средние µ_i;

L_dq – диагональная матрица, полученная из L заменой недиагональных элементов нулями.

Соответственно для среднего времени возвращения в состояние i:

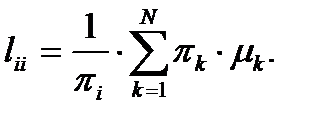(5.3)

Для средней наработки изделия в состоянии j процесса технической эксплуатации между двумя очередными входами в состояние i:

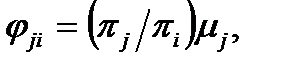
где π_j/π_i – число попаданий в состояние j.

Отсюда следует, что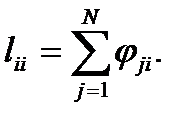

Теорема Смита для конечных процессов с сообщающимися состояниями утверждает, что

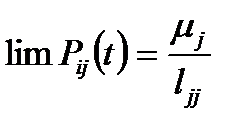(5.4)

Для любых µ_i < ∞ и произвольных функций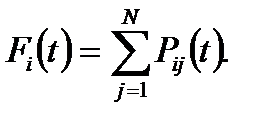

Выражение (5.4) представляет собой коэффициент использования в состоянии j. В частности, если j целевое состояние процесса эксплуатации, то µ_i/l_ii можно определить как целевую функцию процесса технической эксплуатации. Она может рассматриваться как коэффициент готовности, а его максимум может служить критерием оптимальности процесса технической эксплуатации.

Обозначая 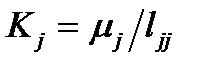и используя выражение (5.3),

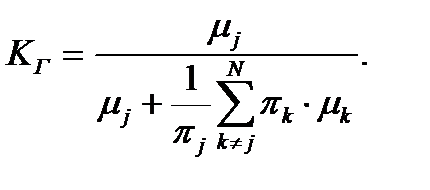(5.5)

Или через наработку t₀ и время ремонта t_в: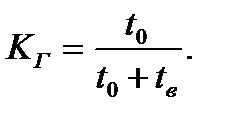

Отсюда следует, что K_j > 0 и 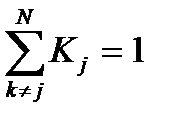. Следовательно, величина K_j (К_Г) имеет вероятностный характер. Так как K_j – функция вероятности P_ik, то она является характеристикой процесса технической эксплуатации и поэтому может служить целевой функцией. Формально этот означает, что максимум K_j может быть принят в качестве одного из критериев оптимальности процесса технической эксплуатации.

Из выражения (5.5) путем несложных алгебраических преобразований можно получить серию широко распространенных на практике удельных критериев эффективности процесса технической эксплуатации, в частности удельные затраты на техническую эксплуатацию. Из выражения (5.5) можно, например, получить

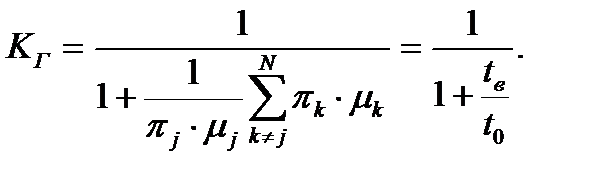(5.6)

Выражение, стоящее в знаменателе (5.6), часто называют коэффициентом средних удельных потерь и обозначают

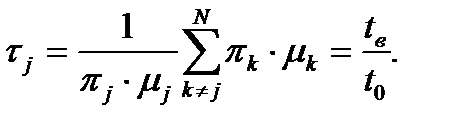(5.7)

Для максимизации K_j в (5.6) достаточно выполнить минимизацию τ_j. Снижение значения τ_j возможно прежде всего за счет перераспределения вероятностей π_j и π_k, а также сокращения µ_k.

В том случае, когда вместо средних времен µ_k введены средние стоимости C_k пребывания в состояниях k=1, 2, …., N, из выражения (5.6) можно получить экономический критерий оптимальности процесса технической эксплуатации и ремонта:

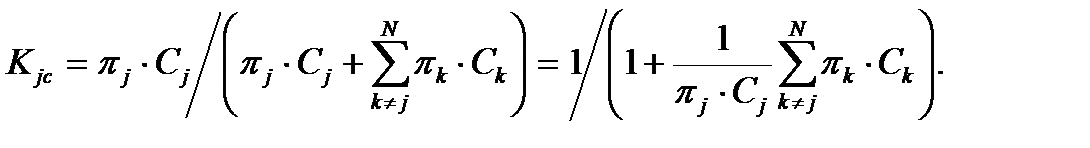(5.8)

Если положить, что производительность в целевом состоянии дает средний удельный доход d_j, то можно считать, что доходы в целевом состоянии 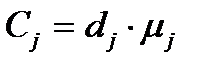. Подставляя это выражение в (5.8),

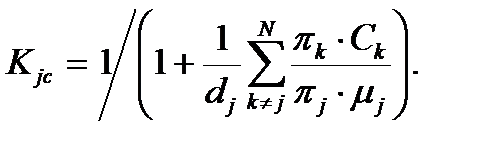
Выражение, определяемое сомножителем при 1/d_j, носит название средних удельных затрат C_j на техническую эксплуатацию и ремонт объекта. Если d_j=const, то максимум K_jc достигается минимизацией выражения:

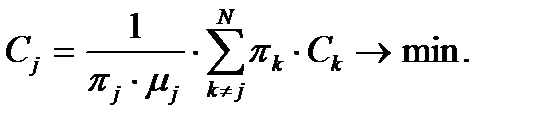(5.9)

Итак, получены целевые функции (5.5) или (5.7) и (5.9). критериями оптимальности процесса технической эксплуатации, следовательно, будут: max K_j (min τ_j) и (или) min C_j. В соответствии с данными критериями ведется поиск оптимальных стратегий технического обслуживания и ремонта применительно к конкретному металлургическому оборудованию.

С помощью диагностирования можно: различить неисправные изделия и подвергнуть их обслуживанию и ремонту; в неисправных изделиях локализовать неисправные узлы и подвергать их обслуживанию и ремонту; в блоках выявлять неисправные элементы и только их ремонтировать и т. д. Чем глубже оценивается техническое состояние, тем более эффективна стратегия. Однако на практике внедрение более эффективной стратегии сопряжено с дополнительными затратами на техническое диагностирование. С учетом этих затрат распределение стратегий по степени их эффективности может существенно измениться. Оптимальной в этом случае будет стратегия обслуживания и ремонта, при которой суммарные приведенные затраты окажутся наименьшими.

Удельная стоимость эксплуатации характеризует совокупность всех затрат на деталь за время ее эксплуатации отнесенную к продолжительности эксплуатации Т определяется из выражения [6]:

С_э=(Д+Р+П)/Т_р, (5.10)

где Д – стоимость запасной части, используемой во время ремонта;

Р – затраты на замену объекта (ремонтное воздействие);

П – стоимость прогнозирования срока отказа;

Т_р – прогнозный ресурс детали, определяемый с учетом заданного значения Р(t).

Для определения значений всех компонент данного показателя используется заданное значение вероятности безотказной работы детали Р(t), а при расчете затрат на деталь и ремонтное воздействие Р(t) обеспечивает учет возрастания этих затрат в случае аварийного ремонта.

При прогнозировании срока отказа могут использоваться различные прогнозные модели. Использование каждой из них требует некоторых затрат, которые могут сильно отличаться для одной и той же детали. Кроме этого, каждая прогнозная модель обеспечивает собственное значение расчетного ресурса для заданного значения Р(t).

Стоимость запасной части складывается из затрат на изготовление, доставку и хранение. Известно, что основное количество запасных частей изготавливается на территории предприятия и сразу же используется во время ремонта. В связи с этим можно считать, что в черной металлургии затраты на доставку и хранение отсутствуют. При определении стоимости запасной части также учтено ее увеличение в случае аварийного ремонта. Это вызывается необходимостью срочного изготовления детали. Стоимость детали составит:

Д=С_И∙[Р(t)+А_Д∙(1- Р(t))], (5.11)

где С_И – стоимость изготовления запасной части;

А_Д – коэффициент увеличения стоимости запасной части (затрат на ее изготовление) в случае аварийного ремонта.

Стоимость ремонтного воздействия зависит от его продолжительности и характеристики используемой ремонтной бригады. Ее состав и квалификация определяется деталью и характером выполняемого ремонтного воздействия. При этом необходимо учесть, что продолжительность ремонтного воздействия увеличивается в случае аварийного ремонта по сравнению с плановым. Затраты на выполнение ремонта составляют:

Р=Т_РЕМ∙N_БР∙S_БР∙[Р(t)+А_Р∙(1- Р(t))], (5.12)

где Т_РЕМ – продолжительность планового ремонта по замене объекта;

N_БР – количественный состав ремонтной бригады;

S_БР – средняя тарифная ставка по бригаде;

А_Р – коэффициент, характеризующий возрастание продолжительности ремонта при аварийном отказе детали.

Стоимость прогнозирования находят для среднего объекта генеральной совокупности. Она зависит от вида прогнозной модели и в случае использования диагностической модели определяется из выражения [6]:

П=З_Н+З_П, (5.13)

где З_Н – затраты по определению начальных параметров модели;

З_П – затраты на прогнозирование срока отказа детали.

Определение начальных параметров прогнозной модели предполагает проведение ряда экспериментов, при этом затраты, приведенные к одной детали, составят:

З_Н=З_Е/Z, (5.14)

где З_Е – затраты, необходимые для проведения экспериментов;

Z – количество деталей, для которых прогнозируются сроки отказов.

В общем случае прогнозной модели предполагается, что срок отказа определяется не из одной попытки, а методом последовательного приближения. На каждом шаге приближения оценивается текущее состояние детали и выполняется собственно прогнозирование. Можно считать, что общему случаю прогнозной модели соответствует диагностическая прогнозная модель. При этом стоимость прогнозирования определяется из выражения:

З_П=(Т_Д∙S_Д+ Т_П∙S_П)∙N, (5.15)

где Т_Д – продолжительность операции по оценке текущего технического состояния объекта (диагностики);

S_Д – удельная стоимость выполнения диагностики;

Т_П – продолжительность обработки результатов диагностики и выполнения прогнозирования;

S_П – удельная стоимость обработки результатов диагностики и выполнения прогнозирования;

N – количество контролей при прогнозировании отказа.